Conversion

Now for the main course. Say we have the NFA

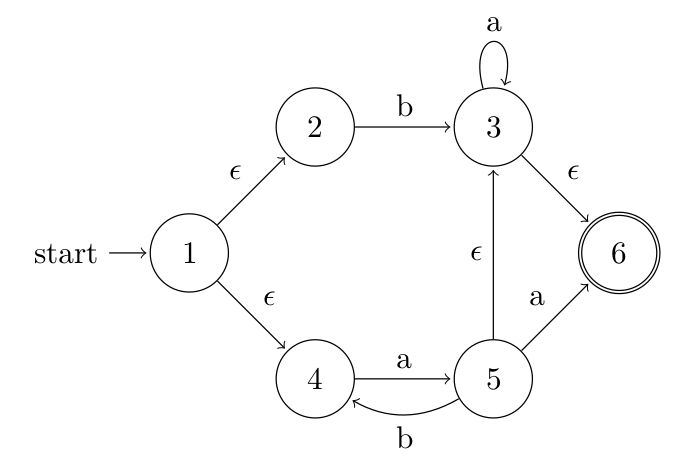
This we want to convert to a DFA (Deterministic Finite Automaton). A DFA is an NFA with the following two properties

No epsilon transitions can be present.
For every transition leaving a state none can have the same symbol.

This can be solved using the following algorithm working on sets. We can easily collect the alphabet as {a,b}. State (1) is the starting state, and the only accepting state is state (6).

For the algorithm we need to calculate what is called an epsilon-closure or ε-closure. We first pick the start state. From this we calculate the ε-closure simply by following every ε-transition that leaves this particular state. We include the state itself and call the result s_{0} = {1,2,4}. From here on we move on every symbol in the alphabet, obtain a new set of states on which we calculate ε-closures and iterate until no new states are added.

move(s_{0},a) = \epsilon({5}) = {5,3,6} = s_{1} move(s_{0},b) = \epsilon({3}) = {3,6} = s_{2} move(s_{1},a) = \epsilon({6,3}) = {3,6} = s_{2} move(s_{1},b) = \epsilon({4}) = {4} = s_{3} move(s_{2},a) = \epsilon({3}) = s_{2} move(s_{2},b) = \epsilon(\emptyset) = \emptyset move(s_{3},a) = \epsilon({5}) = s_{1} move(s_{3},b) = \epsilon(\emptyset) = \emptyset

One important thing to notice is that when we move on a symbol, we do not include the state itself we are moving from. Neither do we move more than once, otherwise infinite moves could be possible. Now we have what's needed to draw the DFA. Each move on a symbol defines a transition, so we get

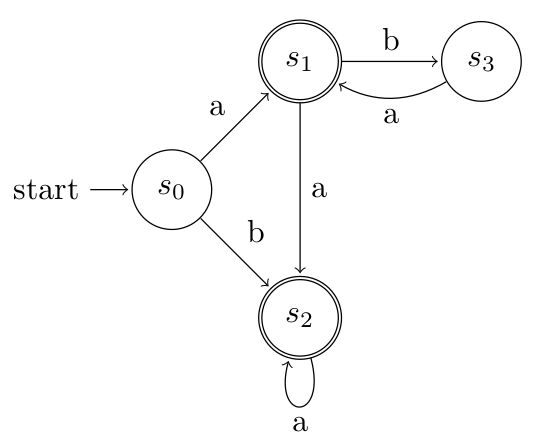
DFA1 - result from converting from NFA1.

Each DFA-state that contains the accepting state (6), is accepting. This algorithm is not easy to get right by hand, I think. Even for relatively simple NFA's I mix up symbols, forget about transitions and so on. Luckily this is an algorithm and hence can be implemented using a programming language. And so I have done which is explained in the last chapter.