Syntax/Input

To actually write any input to the converter we first have to define a suitable syntax. And then we have to make a parser. This might seem circular, we make a parser for creating an NFA with which we can make a parser and so on. But anyway. The parser target (the resulting structure/the converter input) is a Dictionart<string,State> where the state is a tuple of type bool * bool * Transition list : accepting * starting * outgoing transitions.

The lexing is done using Regex.replace replacing the tokens with an empty string and adding the token to a list. If the resulting string isn't empty, garbage is present in the program, and we terminate. We can descibe the tokens as

start = start name = [a-zA-Z0-9]+ line = - rightpointer = > rpar = ) lpar = ( dlpar = (( drpar = )) newline = \n+

And so on. It is important to distinguish between the par-token and the grouping par. The latter is not used. A newline is any number of consecutive newline chars. And spaces are ignored.

I first tried to do the whole parsing using a single regular expression. This is doable, I am pretty sure, but the ungrouping when doing nested grouping in .NET, is abominable. So I instead choose to implement a LL(1) parser. The programming language of choice is F#.

We need a set of grammar rules based on an easy to use syntax. For a set of states and transitions this might be usable

start (1) -eps> (2) -eps> (4) (2) -a>(3) -b>(4) . . . ((6))

And so on. Each new line defines a new state. The -name> is a transition, and ((name)) means accepting state. Perfect. Let us now write the grammar

Exp \rightarrow Exp' Exp' \rightarrow Pre Trans newline Exp' | \epsilon Pre \rightarrow start PreState | PreState PreState \rightarrow State | FinalState Trans \rightarrow -name> State Trans | \epsilon State \rightarrow (name) FinalState \rightarrow ((name))

Left recursion is removed beforehand. PreState is needed since (1) -something> ((6)) might as well result in a syntax error. Note that (what I found out when I started implementing) we have to treat (( and )) as single tokens in order to avoid ambiguity when the parser has to choose productions. Also non-empty Exp' has to end with a newline token

Nullable is right away as

Nullable(Exp) = Nullable(Exp') = true Nullable(Exp') = true Nullable(Pre) = false \lor Nullable(PreState) = false Nullable(PreState) = Nullable(State) \lor Nullable(FinalState) = false Nullable(Trans) = true Nullable(State) = false Nullable(FinalState) = false

First we get as

First(Exp) = First(Exp') First(Exp') = First(Pre) = {start,(,((} First(Pre) = {start,(,((} First(PreState) = First(State) \union First(FinalState) = {(,((} First(Trans) = {-} First(State) = {(} First(FinalState) = {((}

OK. Now for that loathsome Follow-set. We add a start production

S \rightarrow Exp $ Exp \rightarrow Exp' Exp' \rightarrow Pre Trans newline Exp' | \epsilon Pre \rightarrow start PreState | PreState PreState \rightarrow State | FinalState Trans \rightarrow -name> State Trans | \epsilon State \rightarrow (name) FinalState \rightarrow ((name))

We get

{$} \subset Follow(Exp) Follow(Exp) \subset Follow(Exp') {newline} \subset Follow(Trans) First(Trans) \subset Follow(Pre) Follow(Pre) \subset Follow(PreState) Follow(PreState) \subset Follow(State) Follow(PreState) \subset Follow(FinalState) First(Trans) \subset Follow(State)

We iterate

Follow(Exp) = {$} Follow(Exp') = {$} Follow(Trans) = {newline} Follow(Pre) = {-} Follow(PreState) = {-} Follow(FinalState) = {-} Follow(State) = {-}

Hopefully close enough.

LookAhead is what we now obtain

la(S \rightarrow Exp $) = First(Exp) = {start,(,((} la(Exp \rightarrow Exp') = First(Exp') \union Follow(Exp) = {start,(,((,$} la(Exp' \rightarrow Pre Trans newline Exp') = First(Pre) = {start,(,((} la(Exp' \rightarrow \epsilon) = Follow(Exp') = {$} la(Pre \rightarrow start PreState) = {start} la(Pre \rightarrow PreState) = First(PreState) = {(,((} la(PreState \rightarrow State) = {(} la(PreState \rightarrow FinalState) = {((} la(Trans \rightarrow -name> State Trans) = {-} la(Trans \rightarrow \epsilon) = Follow(Trans) = {newline} la(State \rightarrow (name)) = {(} la(FinalState \rightarrow ((name))) = {((}

Now before we implement, it might be worth noting what resulting structure the grammar actually emits. For the nfa

start (1) -eps>(2) -a>(3) ((2))

We can draw the resulting tree as

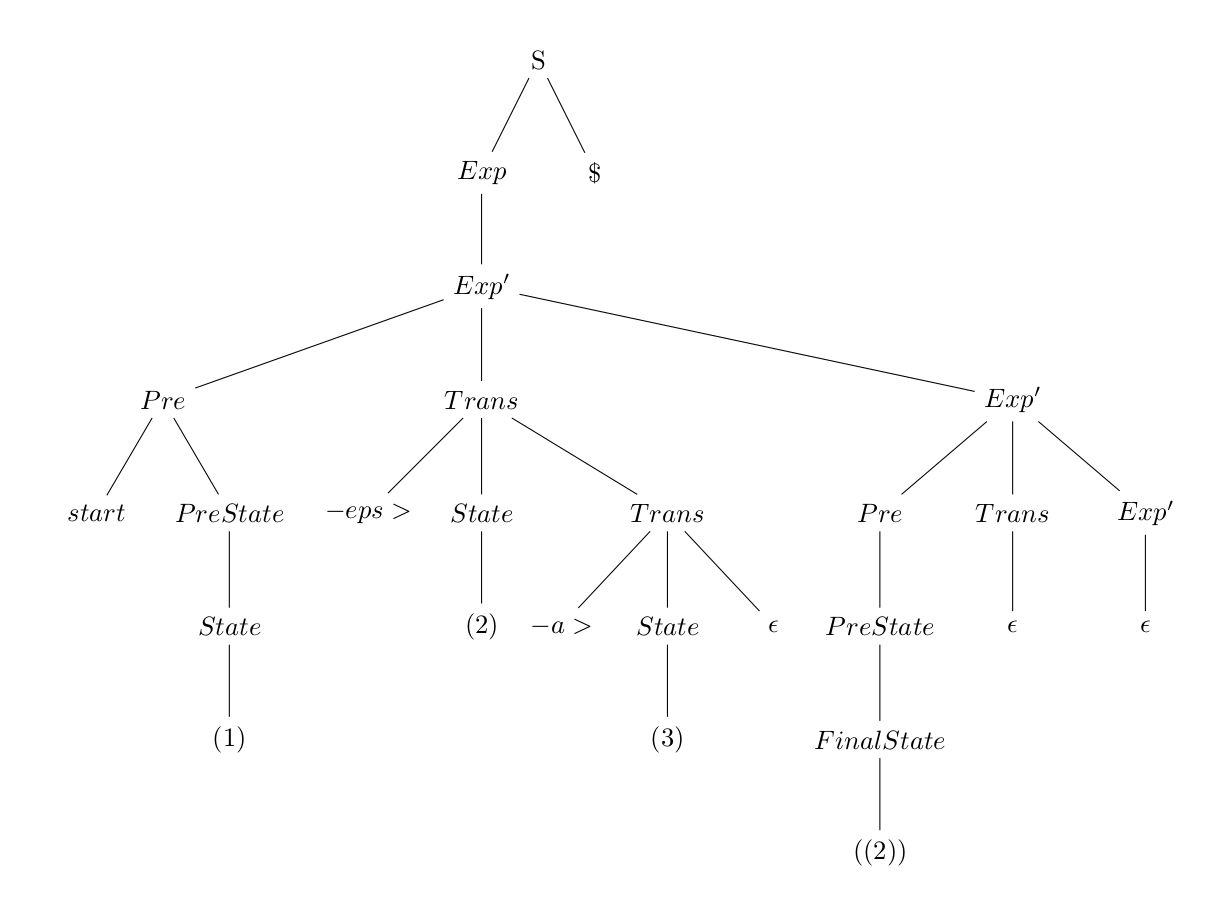
Bearing this in mind we can design the implementation. However, since the target is a dictionary, we might as well let the parser insert every Exp directly. As I have done before: we need to keep track of iteration through the tokens. For this we use a match function, here matchF

let matchF i input = let mLen tl = len - i - tl > 0 match input with | Start when mLen 1 -> (i+1,tokens.[i+1],"") | LPar when mLen 3 -> match (tokens.[i],tokens.[i+1],tokens.[i+2]) with | (LPar,Name stateName,RPar) -> (i+3,tokens.[i+3],stateName) | tError -> errorM (StateError tError) | DLPar when mLen 2 -> match (tokens.[i],tokens.[i+1],tokens.[i+2]) with | (DLPar,Name stateName,DRPar) -> (i+3,tokens.[i+3],stateName) | tError -> errorM (FinalStateError tError) | Line when mLen 3 -> match (tokens.[i],tokens.[i+1],tokens.[i+2]) with | (Line,Name tChar,RightPointer) -> (i+3,tokens.[i+3],tChar) | tError -> errorM (TransitionError tError) | Newline when mLen 1 -> (i+1,tokens.[i+1],"") | Dollar -> (len-1,tokens.[len-1],"") | Epsilon -> (i,input,"") | _ -> errorM (GeneralError tokens.[i..])

We are constructing a LL(1) parser meaning that we look 1 token ahead. Since the grammer mainly contains series of three tokens, the matchF is designed to take care of the extra look ahead. Finally the set of mutually recursive productions

let rec parseS i input startAtt = match input with | Start | LPar | DLPar -> let (i,input) = parseExp i input startAtt let (i,input,_) = matchF i Dollar (i,input) | _ -> errorR input and parseExp i input startAtt = match input with | Start | LPar | DLPar | Dollar -> let (i,input) = parseExp' i input startAtt (i,input) | _ -> errorR input and parseExp' i input startAtt = match input with | Start | LPar | DLPar -> let (i,input,preName) = parsePre i input startAtt let (i,input) = parseTrans i input preName let (i,input,_) = matchF i Newline let (i,input) = parseExp' i input false (i,input) | Dollar -> let (i,input,_) = matchF i Epsilon (i,input) | _ -> errorR input and parsePre i input startAtt = match input with | Start -> let (i,input,_) = matchF i Start let (i,input,name) = parsePreState i input true (i,input,name) | LPar | DLPar -> let (i,input,name) = parsePreState i input false (i,input,name) | _ -> errorR input and parsePreState i input startAtt = match input with | LPar -> let (i,input,name) = parseState i input add2tree (State (startAtt,name)) (i,input,name) | DLPar -> let (i,input,name) = parseFinalState i input add2tree (AcceptingState (startAtt,name)) (i,input,name) | _ -> errorR input and parseTrans i input targetName = match input with | Line -> let (i,input,transChar) = matchF i Line let (i,input,destName) = parseState i input add2tree (Transition (targetName,transChar,destName)) let (i,input) = parseTrans i input targetName (i,input) | Newline -> let (i,input,_) = matchF i Epsilon (i,input) | _ -> errorR input and parseState i input = match input with | LPar -> let (i,input,name) = matchF i LPar (i,input,name) | _ -> errorR input and parseFinalState i input = match input with | DLPar -> let (i,input,name) = matchF i DLPar (i,input,name) | _ -> errorR input

Arguments like targetName and startAtt are passed up and down the traversal. This is done so to stay as functional-oriented as possible. The parser in turns uses add2tree

let add2tree = function | State (startAtt,name) -> tree.Add(name,Nfa2Dfa.newState false startAtt []) () | AcceptingState (startAtt,name) -> tree.Add(name,Nfa2Dfa.newState true startAtt []) () | Transition (targetName,c,destName) -> if not (tree.ContainsKey(targetName)) then let msg = sprintf "transition from undefined state (%s)" targetName failwith msg else let s0 = tree.[targetName] let s = s0.start let acc = s0.accepting let ts = s0.transitions let t0 = if c = "eps" then Nfa2Dfa.Epsilon destName else Nfa2Dfa.Char (c,destName) let ns0 = Nfa2Dfa.newState acc s (t0::ts) tree.[targetName] <- ns0

Since the line -eps> (6) results in a syntax error, "transition from undefined state" can't be reached. I'm just a bit paranoid dealing with collections in .NET. The tree is of course an side effect residing at toplevel of the parser function. Since native .NET dictionaries are mutable by default, this is an OK way to handle tree insertion, I think.