Preface

OK. So I have taken the CompilerCourse exam at my university. Though I really like the subject, the exam were mostly about doing algorithms by hand. Me sweating, dripping down in rows after rows of live variables, DFA minimization schemes, 30 year old creaking teak wood chairs and bad faltering tables. All in the middle of a more than 30 year old gym hall probably used daily by drunk teenagers to smoke weed in. I almost developed permanent lower back pain. But the main problem is that doing algorithms by hand, even mildly complex ones, are both error prone and boring. So afterwards I thought I would create some of those algorithm since, after all, they are made for machines, and machines are made to make our lives less miserable.

The first algorithm I would like to create is a converting algorithm that converts what is called an NFA to what is called a DFA. So tag along if your are dealing with this kind of conversion. This "report" contains a short syntax for the application and details about the algorithm used. Lastly the converter can be run right on this side from a browser.

An NFA (Non deterministic Finite Automaton) is a set of states, a set of transitions and an alphabet to mark the transitions. Each transition has one symbol/mark. Free transitions are called epsilon transitions. These are marked with ε. The state set contains one starting state and one or more accepting state. The idea is: given a string read a char from the string. You are placed in a state. You can now move on any transition that has the current char. When you do such a move, read the next char from the input. ε-transitions are free rides, you can move as many as you want to, and none of the moves changes the current char. If you are in an accepting state, you can leave the NFA. If you at some state can't go anywhere with the current char, the NFA might not accept the given string. Might because there can be several transitions on the same symbol from a state.

NFA's are used for various subjects, most notably, I think, they are used to formalize/implement regular expressions. Say we have the regular expression a(a|b)*. This can be expressed as

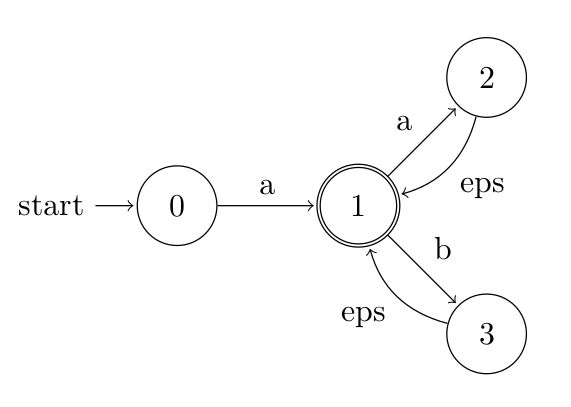
Since an NFA can have several transitions to choose from, every path might have to be examined by a computer to choose the one that accepts a given string. This can require back tracking. Say we switch the ε-transitions with the symbol-marked ones in the graph above. If we are in state 2 and the input char is 'b', we are stuck. But the string might still be acceptable, we can move from (1) to (3) with ε and then back with 'b'. To avoid this ambiguous behavior the NFA can be converted to an DFA in which no two transitions leaving one state can have the same symbol. And this conversion is what we are about to develop an algorithm to do.