We are given some collection \( C \) of records of the form $$ \{key:List\ String,value:Value\} $$ Treat each record as an object. Furthermore treat each \( key \) as a list of words. A word is a string with chars taken from the English alphabet. This can be extended if one wants to.
The heart of Exploding Search is a tree. Each node has the form $$ Node : \{children:Dict\ Char\ Node,results:List\ Ptrs\} $$ Here \( children \) is a dictionary with chars as keys and nodes as values. That is children of the current node. Assume the lookup of this to be constant - since we have char keys we can use an array instead. \( results \) is a list of pointers to a record in \( C \). Now we construct the tree with the following procedure
ConstructTree() root = new Node() curNode = root for record in C do for word in record.key do for symbol in explode(word) do if curNode.children[symbol] == null then curNode.children[symbol] = new Node() curNode.results.Add(record) curNode = curNode[symbol] return rootHere explode("string") is a function that explodes the string into chars. It is from here the algorithm has its name.
Say we want to draw the tree for the following 3 records
rec1 = {key=["rec","one"],val1} rec2 = {key=["rec","two"],val2} rec3 = {key=["last","rec"],val3}We get
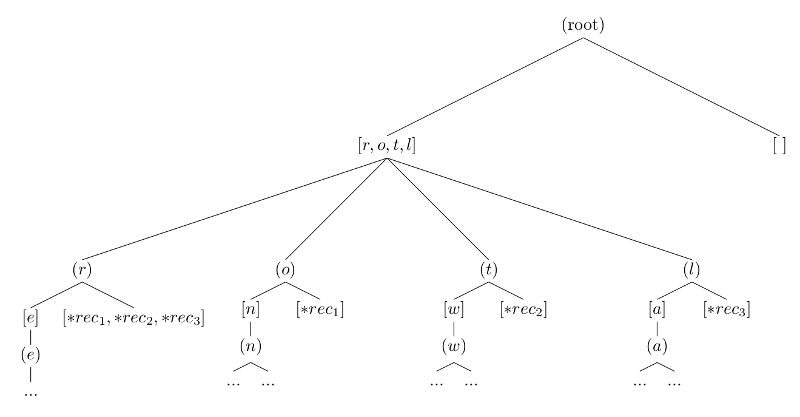
If we in Figure 1 continues down the path of the word "rec", we from the node \( (e) \) have the list \( [c] \) as children. And we have \( [*rec_1,*rec_2,*rec_3] \) as results again.
After the tree has been constructed we simply search by taking a proper path down the tree using the following procedure.
Search(symbol,root) if root.children[symbol] != null then return (root.chilren[symbol],root.children[symbol].results) else return (root,empty result list)Say we search for "swim suit" one letter at the time. This is done as so:
curNode = root (curNode,results) = Search('s',curNode) (curNode,results) = Search('w',curNode) (curNode,results) = Search('i',curNode)Here the final $results$ might contain other records, for example one with "swinging" as key. We can also do this by searching
curNode = root (curNode,results) = Search('s',curNode) (curNode,results) = Search('u',curNode) (curNode,results) = Search('i',curNode)Where we might obtain the extra result with key "sui generis".