5.Co- and Contravariant Hom Functors

Contents/Index

1. Definition
2. Full, Faithful and Embeddings
3. Preserves and Reflects
4. Contra-, Co- and Bivariant
@5. Co- and Contravariant Hom Functors

For the following let $\mathcal{C}$ be a locally small category.

The hom-functor (covariant)

Given $\mathcal{C}$, each object $A$ determines a functor $$ \mathcal{C}(A,-) : \mathcal{C} \rightarrow Set $$ This functor takes each $\mathcal{C}$-object $X$ to the set $\mathcal{C}(A,X)$, that is the set of arrows from $A$ to $X$. Furthermore the functor takes each $\mathcal{C}$-arrow $f : X \rightarrow Y$ to the function $$ \mathcal{C}(A,f) : \mathcal{C}(A,X) \rightarrow \mathcal{C}(A,Y) $$ given as $$ \mathcal{C}(A,f)(g : A \rightarrow X) = f \circ g $$ where the right side composition, $f \circ g$, is in $\mathcal{C}$. $\mathcal{C}(A,-)$ is called a hom-functor. This is sketched in Figure 1.

Proof of functor

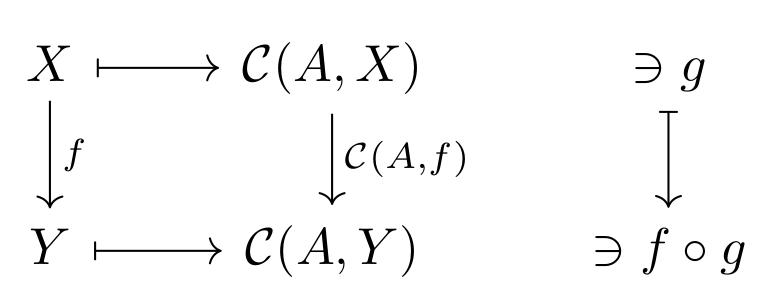
We can prove that the above is a functor. Fix the object $A$. Let objects $X,Y$. All in $\mathcal{C}$. Let $F$ be shorthand for $\mathcal{C}(A,-)$, that is $F(X) = \mathcal{C}(A,X)$ and for $f : X \rightarrow Y$ in $\mathcal{C}$ we have that $F(f) = \mathcal{C}(A,X) \rightarrow \mathcal{C}(A,Y)$. Now let $f : X \rightarrow Y$ and $g : Y \rightarrow Z$ in $\mathcal{C}$. And we get $$ F(g \circ f) = \mathcal{C}(A,X) \rightarrow \mathcal{C}(A,Z) $$ and $$ F(g) F(f) = (\mathcal{C}(A,Y) \rightarrow \mathcal{C}(A,Z)) (\mathcal{C}(A,X) \rightarrow \mathcal{C}(A,Y)) $$ and hence $$ F(g) F(f) = \mathcal{C}(A,X) \rightarrow \mathcal{C}(A,Z) = F(g \circ f) $$ Furthermore we have that $$ F(id_X) = \mathcal{C}(A,X) \rightarrow \mathcal{C}(A,X) = id_{F(X)} $$

Contravariant hom-functor

The contravariant hom-functor is defined as $$ \mathcal{C}(-,B) : \mathcal{C}^{op} \rightarrow Set $$ that takes each object $X$ to the set $\mathcal{C}(X,B)$. Each arrow $h : X \rightarrow Y$ is taken to the function $$ \mathcal{C}(h,B) : \mathcal{C}(X,B) \rightarrow \mathcal{C}(Y,B) $$ given as $$ \mathcal{C}(h,B)(g : X \rightarrow B) = g \circ h $$ As shown in Figure 2. Note that since $h \in \mathcal{C}^{op}$, we have the reverse version as $h : Y \rightarrow X \in \mathcal{C}$. Hence we have that $ g \circ h \in \mathcal{C}(Y,B)$.

Natural relation between covariant and contravariant

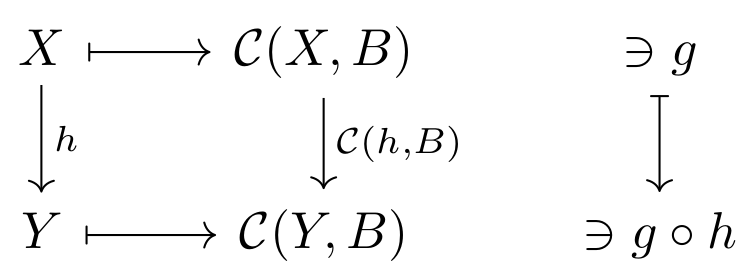
The two above are related in a natural manner. That is for every $\mathcal{C}$-arrows $f : B \rightarrow B'$ and $h : A' \rightarrow A$ the following diagram commutes

Bivariant hom-functor

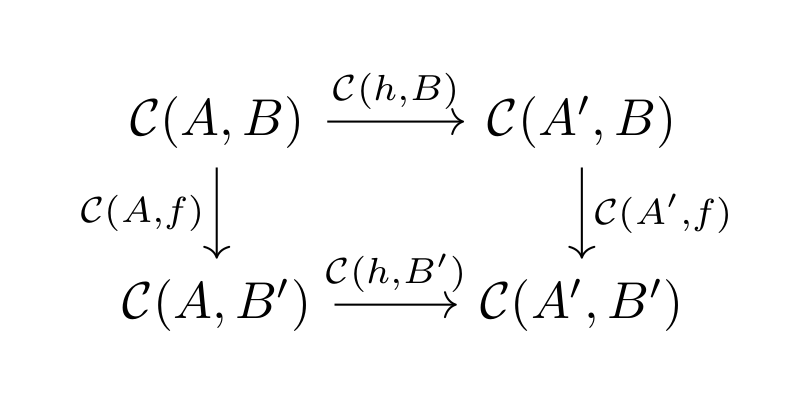
The bivariant hom-functor is for objects defined as $$ \mathcal{C}(-,-) : \mathcal{C}^{op} \times \mathcal{C} \rightarrow Set $$ This is just a composite of the two above functors.