1.Definition and Examples

Contents/Index

@1. Definition and Examples

A natural transformation is a map between two functors that preserves structure. That is let $\mathcal{C}$ and $\mathcal{D}$ be categories. Let $F,G : \mathcal{C} \rightarrow \mathcal{D}$ be functors between these categories. A natural transformation is a a function that assigns to every $\mathcal{C}$-object, $A$, the $\mathcal{D}$-arrow $\mu_A : F(A) \rightarrow G(A)$, such that for every $\mathcal{C}$-arrow, $f : A \rightarrow B$, the following diagram commutes:

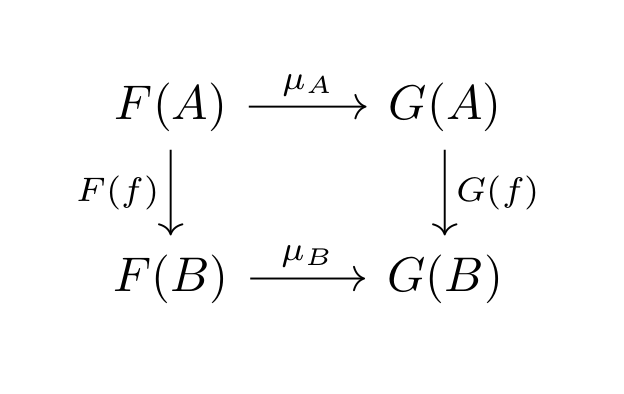
Note that $\mu$ is a set (or family) of arrows - these are indexed by objects of $\mathcal{C}$. That is we can extend the diagram above with nodes $F(C) \rightarrow G(C)$ - this arrow is named $\mu_C$. Also note that all components of the above diagram are in $\mathcal{D}$. That is the family $\mu$ alongside the objects $F(A),F(B),F(C), \dots$ alongside the arrows mapped by the functors $F(f),G(f)$ for $f$ arrow in $\mathcal{C}$.

Example - The monoid category

Recall that the single object monoid category has arrows as elements and a single object representing the underlying set. Functors between two such categories are monoid homomorhisms. Given two such functors $F,G : M \rightarrow N$, natural transformations are $N$-arrows $n$ such that $$ n F(x) = G(x) n $$ for all $M$-arrows $x$. Again $n$ is a family of arrows.

We can make this example more concrete. Let $M = (\mathbb{N},+)$, arrows of this category is whole numbers $0, 1, \dots$, and arrow composition is given as $+$. Let $N = (1^{*},\oplus)$ where $\oplus$ is string concatenation, this is seen as arrow composition. $\epsilon$ is the empty string, and $1^{*} = \epsilon,1,11,111, \dots$ are arrows of $N$. Let $F : M \rightarrow N$ be the functor that creates a string of ones of length $l \in \mathbb{N}$. Let $G : M \rightarrow N$ the functor that creates a string of ones of length $2l$ for $l \in \mathbb{N}$. We now have the family of $N$-arrows: $$ n : F(\mathbb{N}) \rightarrow G(\mathbb{N}) $$ such that $$ F(m) \oplus n_1 = n_2 \oplus G(m) $$ for all $M$-arrows $m$. For example let $m = 2$, let $n_2 = \epsilon$, and let $n_1 = 11$. Remember that we have switched composition for concatenation, these have different order of application. The above states that the corresponding diagram commutes.

Example - Between arbitrary category and preorder

Let $\mathcal{P}$ a preorder regarded as a category. Let $\mathcal{C}$ be an arbitrary category. Let $S,T : \mathcal{C} \rightarrow \mathcal{P}$ be functors. There is a unique natural transformation $\tau : S \rightarrow T$ if and only if $S(C) \leq T(C)$ for every $\mathcal{C}$-object $C$. We can show this:

• Right direction: Let $\tau : S \rightarrow T$ a unique natural transformation. Given any $\mathcal{C}$ object, $C$, we have the $\mathcal{P}$-arrow $$ \tau_C : S(C) \rightarrow T(C) $$ since $\tau$ is a natural transformation. Since $\tau_C \in \mathcal{P}$ (which is a preorder), we know that no co-arrows are present. Hence $S(C) \leq T(C)$ for every $\mathcal{C}$-object $C$.
• Left direction: Let $S(C) \leq T(C)$ for every $\mathcal{C}$-object $C$. That is we know that the unique arrow $$ \tau_C : S(C) \rightarrow T(C) $$ for every object $C$ in $\mathcal{C}$, exists in $\mathcal{D}$.

Example - Between two preorders

Let $P_1,P_2$ be preorders regarded as categories. We can exemplify the above proven statement. Let $S,C : P_1 \rightarrow P_2$ be functors. Say that $S(C) \leq T(C)$ for every $P_1$ object $C$. We make it more concrete. Let $P_1$ be the category of regular expressions of the form $\alpha^{*}$ as objects, here $\alpha$ is just a letter of the English alphabet. For example the object $b^{+}$ is any number of one or more $b$'s. The preorder is given as the order of the letters, so we have an arrow $f : a^{+} \rightarrow b^{+}$. Let objects in $P_2$ be any infinite subset of $\mathbb{N} \setminus \{0\}$. We order the objects by their smallest element. For example $\{2,3,4,\dots\} \leq \{3,4,\dots\}$. Let $S$ be the functor that maps each string of an object $\alpha^{+}$ into the length of this string multiplied by the alphabet index of the object starting from 1. That is $a$ has index 1, $b$ has index 2 and so on. So we have $S(c^{*}) = \{3,6,9,\dots\}$. Let $T$ be the functor that maps into the length times 2 times the alphabet index, so we have $T(c^{*}) = \{6,12,,18,\dots\}$. This is an example of $S(C) \leq T(C)$.

Now we have a unique natural transformation $$ \tau : S(C) \rightarrow T(C) $$ for any $P_1$ object $C$. For example we have the two $P_2$ arrows $$ \tau_a : S(a^{+}) \rightarrow T(a^{+}) $$ and $$ \tau_b : S(b^{+}) \rightarrow T(b^{+}) $$ ... $$ \tau_z : S(z^{+}) \rightarrow T(z^{+}) $$ We have the $P_2$ arrows $$ S(f) : S(a^{+}) \rightarrow S(b^{+}) $$ and $$ T(f) : T(a^{+}) \rightarrow T(b^{+}) $$ and we have that $$ \tau_b \circ S(f) = T(f) \circ \tau_a $$

Example - The reverse list function

In functional programming languages we have the function $rev$ that reverses the elements of a list. That is $$ rev([1,2,3]) = [3,2,1] $$ This function works on any type of list - it is polymorphic. We can compose it with the $map$ function on lists. That is $$ map_f (rev[e_1,e_2,e_3]) = [f(e_3),f(e_2),f(e_1)] $$ Now $map$ is a functor between the category of lists of different types. For example we have a map given as $$ map : List\ String \rightarrow List\ Int $$ This might map a list of strings into a list of lengths of these strings. In this example we have $f(s) = length(s)$. In more general terms if we have $f : S \rightarrow T$, then $$ rev_{T} \circ map_f = map_f \circ rev_S $$ Hence $rev$ is a natural transformation.

Example - Trees and Strings

This example is related to the core idea of the project Interleaving Models in Category Theory. Let $\mathcal{G}$ be the category of labeled, directed graphs. In general we say that two such graphs are isomorphic if they have exact same structure though maybe different labeling. For this example we do not care about state names. So for example given the graph in Figure 2. Name this graph $Gr_1$. We can obtain an isomorphic graph to this with the label mapping $$ t_1 : Gr_1 \rightarrow Gr_2 $$ that rotates every label 2 letters forward: $$ t_1 = [a \mapsto c, b \mapsto d] $$ To keep it simple say that each label is a lower case letter from the English alphabet. So in $\mathcal{G}$ the graphs are objects, and the isomorphic transformations are arrows. The id-arrow is the one that given a graph do not do relabeling.

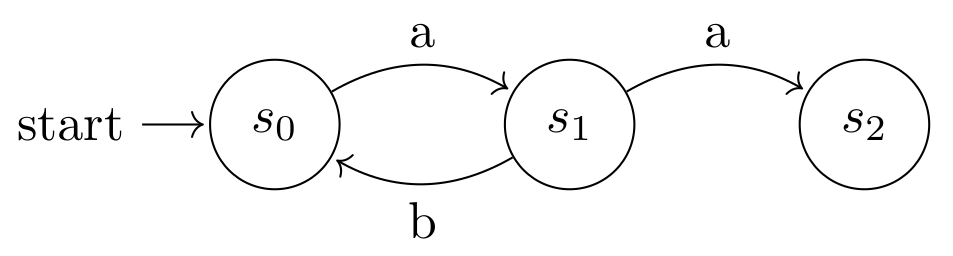
Let $\mathcal{S}$ be the category where the objects are set of strings formed by concatenating lower case letters from the English alphabet. Arrows are character based replacements, that is given the object {"abab","aa"} we have an arrow to the object {"gdgd","gg"}. We have a functor $$ F : \mathcal{G} \rightarrow \mathcal{S} $$ that follows any path and concatenates symbols into a string in order to form objects. For the graph in Figure 2 we have the string set {"","a","aa","ab",...}. Name this string set $S_1$. The arrows are translated directly. We have the $\mathcal{S}$-arrow $$ \eta_1 : S_1 \rightarrow S_2 $$ given as $$ \eta_1 = [a \mapsto e, b \mapsto f] $$ $S_2$ is the same set of strings as $S_1$, but with characters rotated 4 positions. We have that $$ F(t_1) : S_1 \rightarrow S_3 $$ where $S_3$ is the same object as $S_1$ but with each character rotated 2 positions forward. Now we construct the functor $$ G : \mathcal{G} \rightarrow \mathcal{S} $$ that translates objects the same way as $F$, but furthermore each label is rotated 4 positions forward. So we have that $G(Gr_1) = S_2$, and we have that $$ G(t_1) : S_1 \rightarrow S_2 $$ Lastly let $$ \eta_2 : S_3 \rightarrow S_2 $$ be the arrow that rotates two positions, but as follows $$ \eta_2 = [c \mapsto e, d \mapsto f] $$ And we finally have that $$ \eta_2 F(t_1) = G(t_1) \eta_1 $$ This sort of scales into a family. If we see the rotation as modulo the alphabet size, we have a finite number of $\eta$'s. We can chain the $\mathcal{G}$ arrows $t$, that is: $$ t_1 = [a \mapsto c,b \mapsto d], t_2 = [c \mapsto e, d \mapsto f] , \dots $$ up till the last letter of the alphabet is reached. After which we can start over if new letters are mapped.

Note that we for $F$ and any two graphs, $Gr_1,Gr_2$, have that $$ F : \mathcal{G}(Gr_1,Gr_2) \rightarrow \mathcal{S}(F(Gr_1),F(Gr_2)) $$ is a surjection. That is every arrow in $\mathcal{S}(F(Gr_1),F(Gr_2))$ can be target by some arrow in $\mathcal{G}(Gr_1,Gr_2)$. This map is also injective. Hence it is full and faithful. Furthermore the map is injective on objects, hence it is an embedding. However two differently structured graphs can emit the same set of strings. So we see $\mathcal{S}$ as embedded in $\mathcal{G}$.