The adjoint pair of functors ST2TS and TS2ST

Contents/Index

Introduction
Interleaving Models
The adjoint pair of functors HL2ST and ST2HL
@The adjoint pair of functors ST2TS and TS2ST

In this section we will develop an adjoint between the two categories $\textbf{TS}$ and $\textbf{ST}$. As above: We do this by constructing appropriate functors which forms the diagram of the adjoint. Lastly we will look at how one of these categories is embedded in the other.

The functors ST2TS and TS2ST

First we turn our attention to the functor $TS2ST$. Given $$ TS_1 = (S_{TS_1},s^{I}_{TS_1},Trans_{TS_1},L_{TS_1}) $$ One approach is to construct the functor using $HL2ST$ by adding a $TS2HL$. However using this method on $TS_1$ will result in $ST_2$ from which we can't get back to $TS_1$. We simply have lost the information about the cyclic transitions in the original structure.

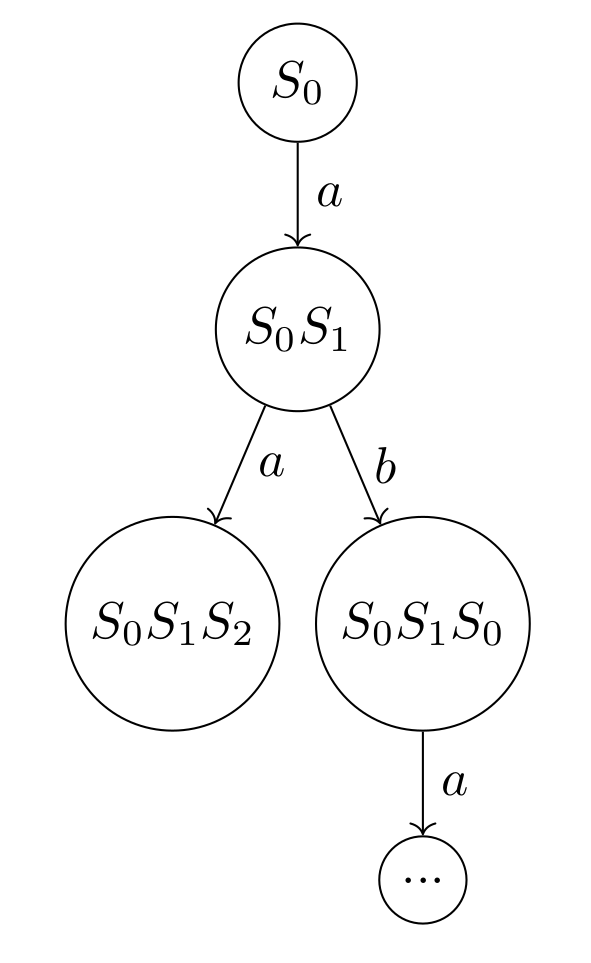
Another approach is to construct $TS2ST$ by naming each state of the resulting $ST$ with the string formed by concatenation of each of the names of the subsequent states. This will ensure that we store enough information to obtain any given $TS$ mapped through $ST2TS \circ TS2ST$. We get $$ TS2ST(TS_1) = (S'_{TS_1},s^{I}_{TS_1},Trans'_{TS_1},L_{TS_1}) $$ where $$ S'_{TS_1} = \{ s_0 s_1 \cdots s_i | \exists s_i \in S_{TS_1} : s_0 \xrightarrow{a_0} \cdots \xrightarrow{a_{i - 1}} s_i \} $$ and $$ Trans'_{TS_1} = \{ (\bar{s}s,a,\bar{s}ss') | \bar{s}s,\bar{s}ss' \in S'_{TS_1}, s \xrightarrow{a} s' \in Trans_{TS_1} \} $$ Given $TS_1$ we obtain $TS2ST(TS_1)$ as shown in Figure 8. Name this $ST_4$

Since $ST$ is a subcategory of $TS$, that is $ST \in \textbf{ST} \Rightarrow ST \in \textbf{TS}$, we can see the functor $ST2TS$ as the identity functor. However if we map down from the last symbol of the name of the state of a given $ST$, we obtain the original $TS$ with possible cycles. That is $$ ST2TS(ST_1) = (S'_{ST_1},s^{I}_{ST_1},Trans'_{ST_1},L_{ST_1}) $$ where $$ S'_{ST_1} = \{ s' | \bar{s} s' \in S_{ST_1} \} $$ with the possibility that $\bar{s} = \epsilon \lor s' = \epsilon$, and $$ Trans'_{ST_1} = \{ (s,a,s') | s,s' \in S'_{ST_1},\bar{s}s \xrightarrow{a} \bar{s}ss' \in Trans_{ST_1} \} $$ Now we have that $ST2TS(TS2ST(TS_1)) = TS_1$. Or in general that $$ ST2TS \circ TS2ST = id_{TS} $$ In general this does not hold the other way around. That is there exists a $ST_i$ such that $$ TS2ST \circ ST2TS \neq id_{ST_i} $$ As an example of why this fails observe the following, we have that $$ ST2TS(ST_2) = TS_{ST_2} $$ that is the exact same tree, but regarded as an object in $\textbf{TS}$. Now we have that $$ TS2ST(TS_{ST_2}) = ST_4 $$ and that $$ ST_4 \neq ST_2 $$

How ST2TS and TS2ST forms an adjunction

The above functor gives rise to the natural transformation $$ \eta_{TS_1} : id(TS_1) \rightarrow ST2TS(TS2ST(TS_1)) $$ The diagram of a natural transformation, as given in Figure 7 for $HL2ST \circ ST2HL$, commutes for $\eta_{TS_i}$, since any given arrow, $h' \in \textbf{TS}$, is mapped to itself. That is $$ h' = ST2TS(TS2ST(h')) $$ Finally we get the adjoint shown in Figure 9.

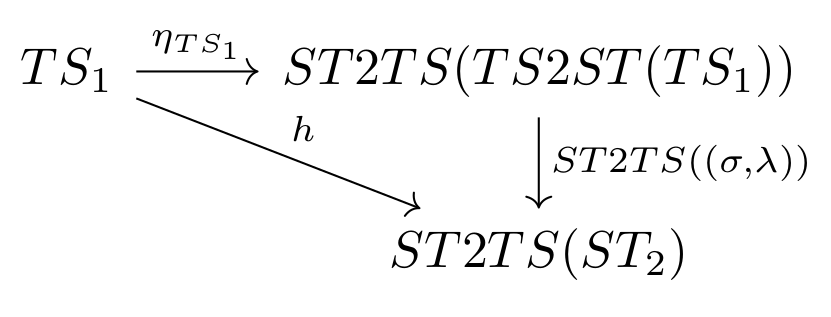
$ST2TS$ is the right adjoint of $TS2ST$ and vice versa.

Embeddings

Since we in general do not have that $TS2ST \circ ST2TS = id_{ST}$, we see $\textbf{ST}$ as embedded in $\textbf{TS}$. The $TS2ST$ functor abstracts away information about the states of the tree, or conversely $\textbf{ST}$ is a more abstract version of $\textbf{TS}$.