Interleaving Models
22.08.2020
Contents/Index
Introduction@Interleaving Models
The adjoint pair of functors HL2ST and ST2HL
The adjoint pair of functors ST2TS and TS2ST
The three models that are studied in this project are called interleaving models. In this section we present the three models and how these are represented as a category. Furthermore we will develop some intuition of the models by examples. These examples are used later when we construct functors and develop adjoints between the different categories of these models.
Labeled Transition Systems
A labeled transition system is a structure $$ TS = (S_{TS},S^{I}_{TS},L,Tran_{TS}) $$ where
- $S_{TS}$ is a set of states.
- $S^{I} \in S_{TS}$ is the initial state.
- $L_{TS}$ is a set of labels.
- $Tran_{TS} \subset S_{TS} \times L_{TS} \times S_{TS}$ is the transition relation.
Given two transition system, $TS_0$ and $TS_1$, an arrow $h : TS_0 \rightarrow TS_1$ is a pair $(\sigma,\lambda)$, where $\sigma : S_{TS_0} \rightarrow S_{TS_1}$ is a function, and $\lambda : L_{TS_0} \rightharpoonup L_{TS_1}$ a partial function, such that:
- $\sigma(S_{TS_0}^{I}) = S_{TS_1}^{I}$, that is $\sigma$ preserves the initial state.
- $(s,a,s') \in Trans_{TS_0}$ implies
- If $\lambda \downarrow a$, then $(\sigma(s),\lambda(a),\sigma(s')) \in Trans_{TS_1}$. The condition $\lambda \downarrow a$ reads as $\lambda$ is defined on $a$.
- Else $\sigma(s) = \sigma(s')$.
We define the category $\textbf{TS}$ of labeled transition systems with $TS_0 , TS_1 , \dots$ as objects and the pair $(\sigma,\lambda)$ as arrows.
Synchronization Trees
A synchronization tree is an acyclic, reachable transition system $ST$ such that $$ (s',a,s),(s'',b,s) \in Trans_{ST} \Rightarrow s' = s'' \land a = b $$ That is we have no two different incoming paths to any node. We denote the category of synchronization trees $\textbf{ST}$ as a subcategory of $\textbf{TS}$.
Examples of Trees
Let us develop some intuition behind the categories $\textbf{TS}$ and $\textbf{ST}$. Say we have the $TS$ as seen in Figure 2. Name this $TS_1$. Regarded as a finite automaton where all states are accepting, this transition system defines the same language as the regular expression $$ (ab)^{*}(a|aa|\epsilon) $$ We can translate $TS_1$ into the $ST$ seen in Figure 3. Name this $ST_1$. $ST_1$ is infinite in size since the language of the corresponding $TS_1$ is infinite. However $TS_1$ is not infinite in size since transition systems are allowed to contain cycles.
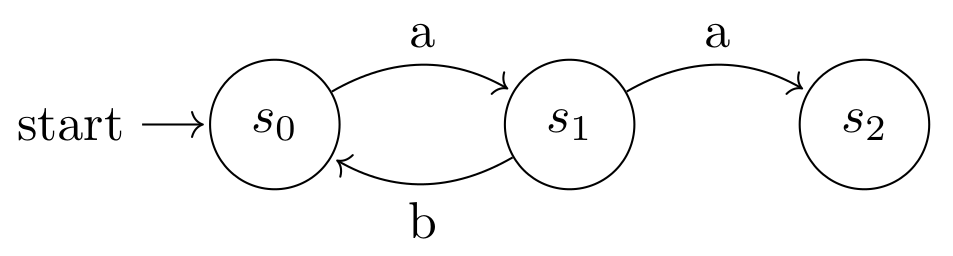
We have that $L_{ST_1} = \{a,b\}$. We have that $s_{ST_1}^I = \{S_0\}$. We have that $S_{ST_1} = \{S_0,S_1, \dots \}$. And we have that $Trans_{ST_1} = \{ (S_0,a,S_1),(S_0,a,S_3), \dots \}$.
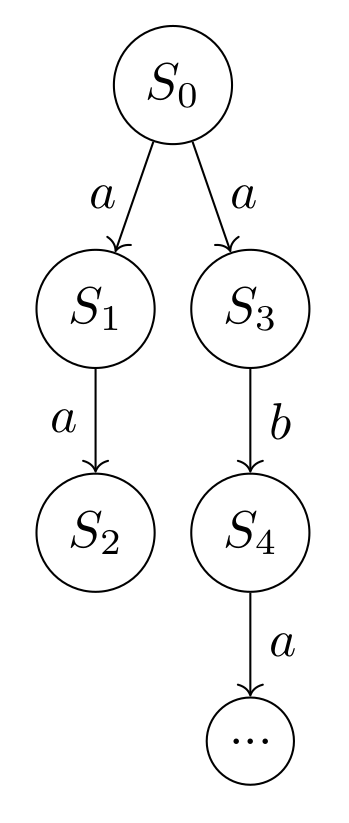
The tree in Figure 3 is one possible tree. We have an arrow $\eta_{ST} = (\sigma,\lambda)$ in $\textbf{ST}$ that translates $ST_1$ into the tree found in Figure 4. Name this $ST_2$. $\eta_{ST}$ is given as $$ \sigma(s_i) = \{ \alpha | s_0 \xrightarrow{a_0} s_1 \xrightarrow{a_1} \cdots \xrightarrow{a_{i - 1}} s_i \land \alpha = a_0 \cdots a_{i - 1} \} $$ That is for each state $s_i \in ST_1$ we translate into a path up till $s_i$. So state $s_i$ after translation is named $$ a_0 \cdots a_{i - 1} $$ For $\eta_{ST}$ we have that $$ \lambda = id $$ since the same set of labels is used.
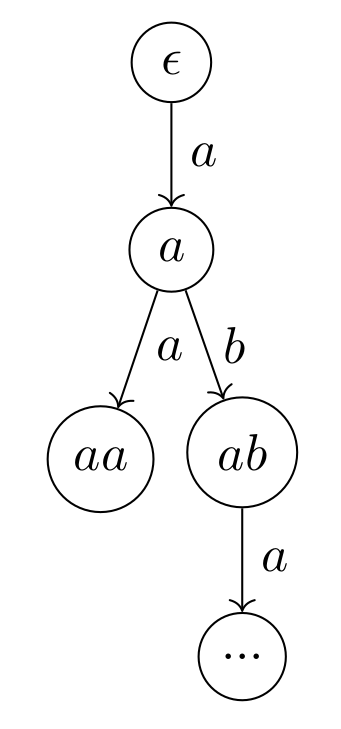
Note that we do not have an arrow in $\textbf{ST}$ from $ST_2$ to $ST_1$. When constructing each new state, $s_{\alpha}$, two adjacent paths that comes from the same parent node and have the same label, are collapsed into one path. We can't use (2) of the definition of arrows in $TS$ to split the state $s_{\alpha}$ into two states. We call the tree of $ST_2$ the canonical form. Later when we discuss adjunctions, we will return to this canonical form.
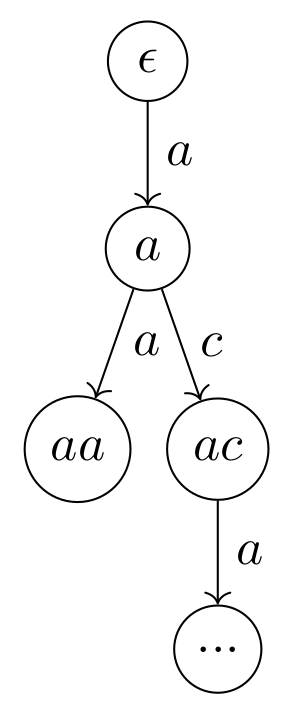
The tree as seen in Figure 5 can be constructed using $ST_1$ with the same translation used to construct $ST_2$, but with $\lambda$ given as $$ \lambda = [a \mapsto a,b \mapsto c] $$ Name this tree $ST_3$.
Hoare Languages
A Hoare language is a pair $HL = (H_{HL},L_{HL})$, here $H_{HL}$ is the set of all strings that can be created within the language, and $L_{HL}$ is the alphabet. A Hoar language satisfies the following two properties
- $\emptyset \neq H_{HL} \subseteq L_{HL}^{*}$.
- $sa \in H_{HL} \Rightarrow s \in H_{HL}$.
A partial map $\lambda : HL_0 \rightharpoonup HL_1$ is a morphism of Hoare languages from $(H_{HL_0},L_{HL_0})$ to $(H_{HL_1},L_{HL_1})$ if for each $s \in H_{HL_0}$ we have $\hat{\lambda}(s) \in H_{HL_1}$, where $\hat{\lambda} : L_{HL_0}^{*} \rightarrow L_{HL_1}^{*}$ is given as
- $\hat{\lambda}(\epsilon) = \epsilon$.
- $\hat{\lambda}(sa) = \begin{cases} \hat{\lambda}(s)\lambda(a) & \text{if } \lambda \downarrow a \\ \hat{\lambda}(s) & \text{otherwise} \end{cases}$
This gives rise to the categori $\textbf{HL}$ of Hoare languages, with $(H,L)$ pairs as objects, and $\lambda$'s as arrows.
Examples using Hoare Languages
Again we can develop some intuition. Say we have $HL_1$. Here we define $$ L_{HL_1} = \{ a,b \} $$ So we have that $L_{HL_1}^{*}$ is every possible finite combination of series of the symbols $a$ and $b$. We let $H_{HL_1}$ match the language of $TS_1$. That is every possible string we can form with $TS_1$. We have that property $ii$ is satisfied, since we can stop in each state in a TS, that is we only travel one symbol at a time. So say we are in state $s_i$ of $S_{TS_1}$. This forms the string $$ \epsilon \cdot a_0 \cdot a_1 \cdots a_{i - 1} \in H_{HL_1} $$ We can do this recursively until the string $\epsilon$ is reached. This corresponds to how we have defined $\sigma$ in arrows of $\textbf{ST}$: the parent of state $s_i$ is named $$ \epsilon \cdot a_0 \cdots a_{i - 2} $$ We create $HL_2$ in the exact same manner, but with $$ L_{HL_2} = \{a,c\} $$ We have an arrow between $HL_1$ and $HL_2$. That is $\lambda_{HL}$ for which $$ \lambda_{HL} = [a \mapsto a,b \mapsto c] $$ Substituting symbols is exactly what $\lambda$ recursively does.