Introduction
22.08.2020
Contents/Index
@IntroductionInterleaving Models
The adjoint pair of functors HL2ST and ST2HL
The adjoint pair of functors ST2TS and TS2ST
In this project we analyse the relationship between Hoare Languages, Labelled Transition Systems and Synchronization Trees seen from a Category Theoretical perspective. These models are collectively known as interleaving models. We are especially interested in the adjoints that arises from defining functors that translates between these structures. These functors reveals how one model is embedded into another in terms of how one model is more abstract than another.
A basic example with the coffee machine
In terms of deterministic behavior the relationship between the language formed by concatenating symbols from an alphabet, and a tree structure can be exemplified as thus: Say we have some machine that serves coffee or tea. This machine can be deterministic after a coin is inserted. That is we are provided with the choice of coffee or tea. Or it can be non-deterministic, that is no one knows the outcome - we might have tea, we might have coffee. This can be modelled in terms of a tree. The left tree in Figure 1 models the deterministic machine, whereas the right tree in Figure 1 models the non-deterministic machine.
We can alternatively choose to model the machine with a language. Here we have an alphabet of symbols we can concatenate to form a string. For our machine we have an alphabet of $$ \{\varepsilon, c, tea, coffee \} $$ In this specific language we have among others the two strings $$ \epsilon \cdot c \cdot tea $$ and $$ \epsilon \cdot c \cdot coffee $$ Since we are restricted by how the machine functions, we do not have the string $$ \epsilon \cdot c \cdot tea \cdot coffee $$ in the language. Furthermore we can't model the non-deterministic version seen in the right tree of Figure 1. That is we can't model what happens after $S_1$ since no one knows. This would require a set as a symbol in the alphabet that is treated as a random variable, for example given as $$ \epsilon \cdot c \cdot \{ tea, coffee \} $$ Hence the above language of strings abstracts away the non-deterministic behavior. However every string of this language can be represented as a tree. So we say that the more abstract language is embedded in the less abstract trees.
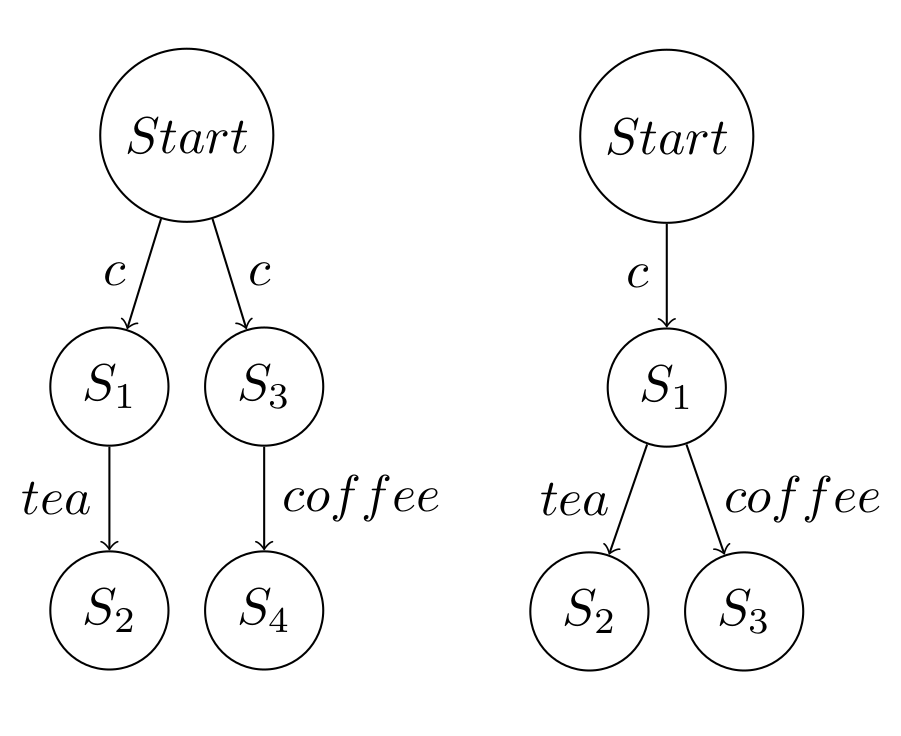
The language of strings is seen as linear. Whereas the language of trees is seen as a branching type.
Background Material
Everything about the interleaving models is taken from the paper "A Classification of Models for Concurrency". These subjects have been elaborated on by my supervisor Thomas Troels Hildebrandt.