The XOR problem as a Neural Network
04.10.2020
This is an example of a simple neural network used to calculate XOR for some input.
Units
A unit is the building block of a neural network. It takes a set of real valued numbers as input, $\mathbb{x}$, computes on them and thereby produces an output. The computation is done as follows: a set of weights, $\mathbb{w}$, is multiplied to the input, and a bias, $b$, is added. That is for $z$ the output $$ z = b + \sum_{i} w_i x_i $$ This can be expressed in vector notation as $$ z = \mathbb{w} \cdot \mathbb{x} + b $$ Finally the output $z$ is applied to some function $f$ - this step is called activation. This final output we name $y$: $$ y = f(z) $$
Activation
We have the following standard activation functions
- $tanh$: given as $$ y = \frac{e^z - e^{-z}}{e^{z} + e^{-z}} $$
- $ReLU$: The simplest and most commenly used. We have $$ y = max(z,0) $$ That is if $z \lt 0$, then $0$, else $z$.
The XOR problem as a neural network
We construct a neural network by connecting these above described units. For each unit we connect to the input of every unit in the next layer. In order to solve the XOR problem we need one layer, called a hidden layer, placed between the input and output layer. Given input $$ x = [x_1 , x_2] $$ We have two units in the hidden layer: $$ h_1 = \{ b = 0,w = [1,1] \} $$ and $$ h_2 = \{ b = -1, w = [1,1] \} $$ And we have an output layer $$ y = \{ b = 0,w = [1,-2] \} $$ At the output of each layer we use the $ReLU$ function. The network is shown in Figure 4.
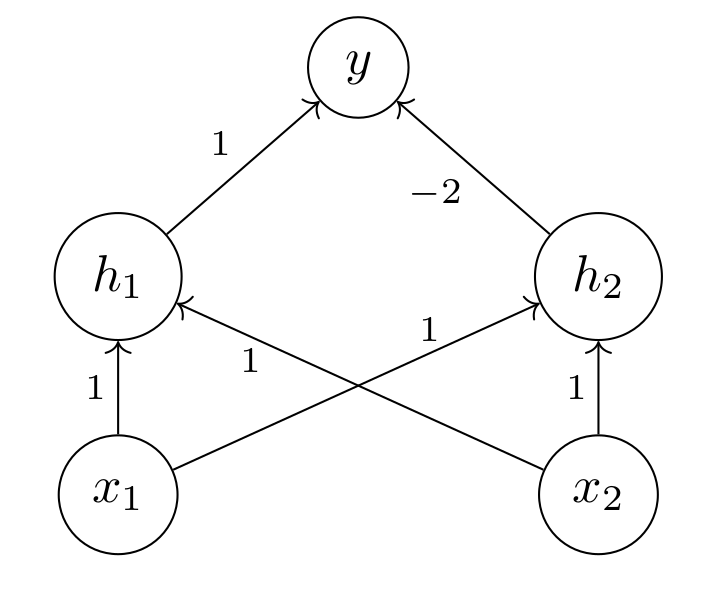
Now we can go through the whole network with different inputs.
- For $x = [0,0]$ into $h_1$ we get $$ [0,0] \cdot [1,1] + 0 = 0 $$ And into $h_2$ we get $$ [0,0] \cdot [1,1] - 1 = -1 $$ after activation we have the vector $$ [0,0] $$ which goes into the output layer $$ [0,0] \cdot [1,-2] + 0 = 0 $$
- For $x = [1,0]$ into $h_1$ we get $$ [1,0] \cdot [1,1] + 0 = 1 $$ into $h_2$ we get $$ [1,0] \cdot [1,1] - 1 = 0 $$ Here the activation does nothing. So we have the vector $[1,0]$ which goes into the output layer, and we get $$ [1,0] \cdot [1,-2] + 0 = 1 $$
- For $x = [0,1]$ we get the exact same result as for $x = [1,0]$.
- For $x = [1,1]$ into $h_1$ we get $$ [1,1] \cdot [1,1] + 0 = 2 $$ Into $h_2$ we get $$ [1,1] \cdot [1,1] - 1 = 1 $$ The activation does nothing. This goes into the output, and we get $$ [2,1] \cdot [1,-2] + 0 = 0 $$
The weights of the hidden layer can be seen as a matrix $$ h_{ws} = \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} $$ The bias of the hidden layer can be seen as a vector $$ h_{bs} = \begin{bmatrix} 0 \\ -1 \end{bmatrix} $$ Furthermore we have that $$ y_{weights} = \begin{bmatrix} 1 \\ - 2 \end{bmatrix} $$ and $$ y_{b} = 0 $$ So given input $x$ we can calculate output of the hidden layer as $$ h_{out} = ReLU(h_{ws} \cdot x + h_{bs}) $$ if we use $ReLU$ for activation.
We can end this by doing a python implementation. We just do matrix multiplication as in the above example for the whole program. We need first import numpy as np. For some reason I can't figure how to flatten the resulting numpy arrays, the result is in 2d. So we need a the following function:
def flatten_a(xs): l = xs.shape[1] res = [] for i in range(0,l): x = xs[0,i] res.append(x) return np.array(res)We can implement the activation as follows
def relu(x): if x.shape == (): return max(x,0) else: return np.maximum(x,np.array([0,0]))And finally we get
def do_xor(x): # weights of hidden layer hws = np.matrix("1 1; 1 1") # bs of hidden layer hbs = np.array([0,-1]) # output weights yws = np.array([1,-2]) # b of output yb = 0 # computations through hidden layer layer_h = x * hws + hbs out_h = relu(flatten_a(layer_h)) # computation throught output layer layer_y = yws.dot(out_h) + yb out_y = relu(layer_y) # return value is an integer/scalar return out_yAnd some testing
# inputs x0 = np.array([0,0]) x1 = np.array([1,0]) x2 = np.array([0,1]) x3 = np.array([1,1]) # print outputs print(do_xor(x0)) # 0 print(do_xor(x1)) # 1 print(do_xor(x2)) # 1 print(do_xor(x3)) # 0And that's it!