Sigmoid Neurons

Given a network of perceptrons we want to train. Say we want it to correctly recognize a picture of a digit. It mistakes a 8 for a 9. We make small corrections in weights until the network recognizes a 9 as a 9. This is a training procedure. The problem occurs if the change we make, makes a perceptron flip. Say from 0 to 1. So we might have a network that can recognize a 9, but the rest of the network might be incorrect in a complicated way. A perceptron can be depicted as a step function:

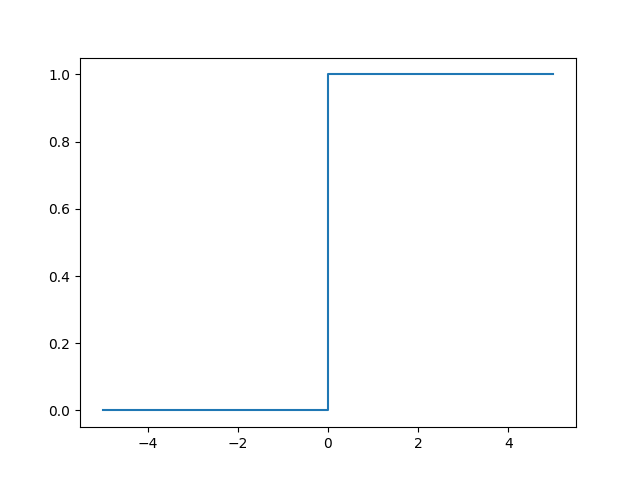
To overcome this problem we introduce sigmoid neurons. These are similar to perceptrons, but instead of a stepping behavior we smooth them. The setup is identical. We have a series of inputs $x_1, x_2 , ...$ and a single output. However inputs and output are real valued in the interval $[0 ... 1]$. Sigmoids have weights, $w_1,w_2 , ...$, as well as an overall bias, $b$. However that output is not binary, but instead calculated as $\sigma(w \cdot x + b)$, where $\sigma$ is called the sigmoid function, and is given as $$ \sigma(z) = \frac{1}{1 + e^{-z}} $$ Again we can plot this function:

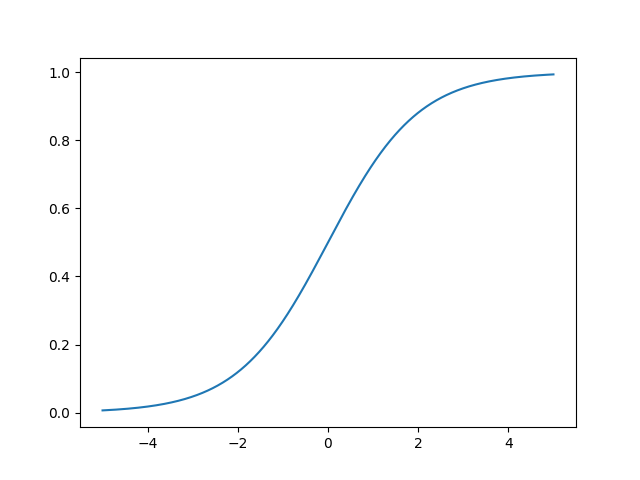
When the argument $z$ is large, we have that $e^{-z} \sim 0$ and thus that $\sigma(z) \sim 1$. On the other hand when $z$ is large and negative, we have that $e^{-z} \sim \infty$. And thus that $\sigma(x) \sim 0$. In between these cases we have a neuron that differs from the perceptron. If we choose a step function as $\sigma$, we do not smooth anymore. Hence the sigmoid would be a perceptron.

Since the sigmoid neuron is smoothed, a small change in weights and bias, $\Delta w_i$ repsectively $\Delta b$ produces a small change in the output, that is a small $\Delta output$. The output change is well approximated by $$ \Delta output \sim \sum_{j} \frac{\partial output}{\partial w_i} \Delta w_i + \frac{\partial output}{\partial b} \Delta b $$

The output from a sigmoid neuron might have to be interpreted. That is a new threshold can be added so that for example everything below 0.7 is 0 and the rest is 1.