Shortest Path

In General

A graph is a set of vertices and a set of edges $G = (V,E)$ with a weight function $w : E \rightarrow \mathbb{R}$ mapping edges to weights.

The weight of a path, $w(p)$, is a sum of the weights of edges on this path $$ w(p) = \sum_{i = 1}^{k} w(v_{i - 1},v_{i}) $$ And we define the shortest path, $\delta(u,v)$, to be $$ \delta(u,v) = \begin{cases} min\{w(p) : u \rightarrow v\} & path(u,v)\\ \infty & else \end{cases} $$

General About Shortest Path Finding

• Shortest path from start point to all destinations.
• Oriented, weighted graphs.
• The problem has optimal substructure:
  • Assume $x \rightarrow y \rightarrow z$ shortest path.
  • Assume that $w(y_1 \rightarrow z_1)$ is less than $(y \rightarrow z)$.
  • Now replace $y \rightarrow z$ with $y_1 \rightarrow z_1$ to obtain a contradiction to the assumption that $x \rightarrow y \rightarrow z$ is a shortest path.

For cycles in graphs we have that if two rounds results in a weight less than that of one round, we can loop for ever to reduce weight, thus obtaining a shortest path weight of $-\infty$.

Relaxing is a common method used within shortest path algorithms. Before we can relax a graph, we iterate the graph adding for each vertex, $v$, the attributes $v.d$ and $v.\pi$, that is shortest path estimate and predecessor, respectively. For this we have

Init-Single-Source(G,s) for each vertex v \in G.V v.d = ∞ v.π = Nil s.d = 0

And the Relax pseudo code is:

Relax(u,v,w) if v.d > u.d + w(u,v) v.d = u.d + w(u,v) v.π = u

The idea is very simple. If a vertex has a larger estimate than the weight of the current edge, update estimate.

Shortest Path Properties

• Triangle inequality For any edge $(u,v) \in E$ we have that $\delta(s,v) \leq \delta(s,u) + w(u,v)$.
• Upper-bound property We always have $v.d \geq \delta(s,v)$ for alle vertices $v \in V$, and once $v.d$ achieves the value $\delta(s,v)$, it never changed.
• No-path property If there is no path from $s$ to $v$, then we always have $v.d = \delta(s,v) = \infty$.
• Convergence property If $s \rightsquigarrow u \rightarrow v$ is a shortest path in $G$ for some $u,v \in V$, and if $u.d = \delta(s,u)$ at any time prior to relaxing edge $(u,v)$, then $v.d = \delta(s,v)$ at all times afterwards.
• Path-relaxation property If $p = \langle v_0, v_1, ..., v_k \rangle$ is a shortest path from $s = v_0$ to $v_k$ and we relax the edges of $p$ in the order $(v_0,v_1),(v_1,v_2),...,(v_{k - 1},v_k)$, then $v_k.d = \delta(s,v_k)$. This property holds regardless of any other relaxation steps that occur, even if they are intermixed with relaxations of the edges of $p$.
• Predcessor-subgraph property Once $v.d = \delta(s,v)$ for all $v \in V$, the predecessor subgraph is a shortest-path tree rooted at $s$.

Dijkstra's Algorithm

The algorithm can't handle negative edges. The algorithm can be implemented very efficiently using a min-heap. The idea is quite simple. Let $S$ some structure to store final shortest paths in. Let $Q$ be a min-priority heap with vertices. We get

Dijkstra(G,w,s) S = \emptyset Q = Heap while Q \neq \emptyset u = ExtractMin(Q) S = S \union {u} for each vertex v \in G.Adj[u] Relax(u,v,w)

Example

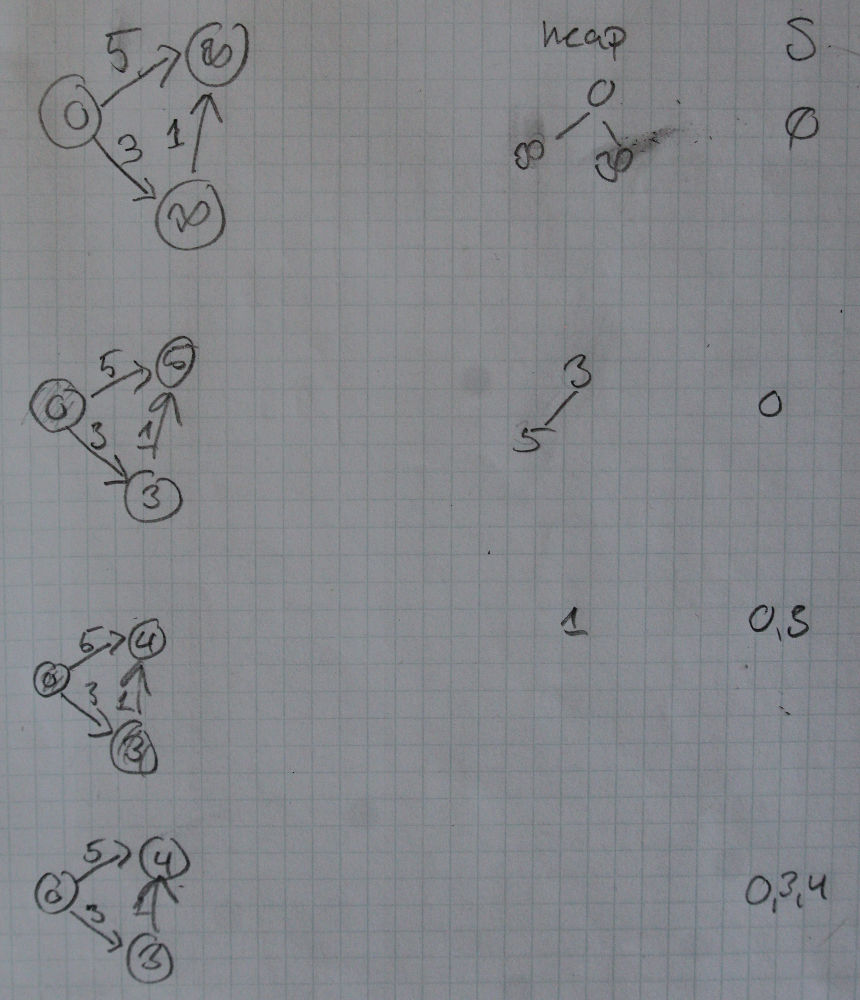
Corectness of Dijkstra's Alg

The proof rely on the shortest path properties. We show by loop invariant that when a vertex estimate, $v$, is added to $S$, then we have that $v.d = \delta(s,v)$. In general $s$ is the very first vertex added to $S$.

• By initialization we have that $S = \emptyset$ which is trivially true.
• Maintenance. We wish to show that in each iteration $u.d = \delta(s,u)$ for the vertex added to $S$. For the purpose of contradiction assume that $u$ is the first vertex added to $S$ where $u.d \neq \delta(s,u)$. We get
  • $u \neq s$ since $s$ is the first vertex added to $S$, and $s.d = \delta(s,s) = 0$.
  • By the above we have that $S \neq \emptyset$ just before $u$ is added to $S$.
  • There must be some path from $s$ to $u$, otherwise $u.d = \delta(s,u) = \infty$ by no-path prop. which violates the assumption that $u.d \neq \delta(s,u)$.
  • Since there is at least one path, there is a shortest path, $p$, from $s$ to $u$.
  • Prior to adding $u$ to $S$, path $p$ connects a vertex in $S$, $s$, to a vertex in $S - V$, $u$.
  • Consider the first vertex $y$ along $p$ such that $y \in V - S$.
  • Let $x \in S$ be $y$'s predecessor along $p$.
  • We can decompose path $p$ into $s \rightsquigarrow x \rightarrow y \rightsquigarrow u$.
  • We claim that $y.d = \delta(s,y)$ when $u$ is added to $S$. Proof: Observe that $x \in S$. Since $u$ is the first vertex added where $u.d \neq \delta(s,u)$, we have that $x.d = \delta(s,x)$ when $x$ was added to $S$. Edge $(x,y)$ was relaxed at that time, and we conclude using the convergence property.
  • Contradiction is now obtained.
  • Since $y$ appears before $u$ on a shortest path from $s$ to $u$ and all edge weights are non-negative, we have $\delta(s,y) \leq \delta(s,u)$ and thus $y.d = \delta(s,y) \leq \delta(s,u) \leq u.d$ (upper bound prop).
  • But we also have that $y$ and $u$ were in $V - S$ when $u$ was chosen: we have that $u.d \leq y.d$ and thus the equality $y.d = u.d$.
  • Finally we have that $u.d = \delta(s,u)$ which is absurd compared to our original assumption.
• Termination. At termination we have that $Q = \emptyset$ which along with earlier invariants that $Q = V - S$ implies that $S = V$.

By all this we have that Dijkstra's alg results in a set, $S$, of shortest paths.

Running time

Implemented with a min priority heap we have a time complexity of $O((V + E) lg V) = O(E \cdot lg V)$. That is: we iterate $E$ times, and for each iteration we do a decrease key that takes time $O(lg V)$. We can optimize this a bit by using a fib-heap. In this case we get $O(V \cdot lg V + E)$.

Bellman/Ford alg

This algoright can detect and report negative cycles. The code is

Bellman-Ford(G,w,s) Init-Single-Source(G,s) for i = 1 to |G.V| - 1 for each edge (u,v) \in G.E Relax(u,v,w) for each edge (u,v) \in G.E if v.d > u.d + w(u,v) return False return True

Running Time of Bellman/Ford

init-single-source is $O(V)$. The first for-loop executes $O(V)$ times, which for each there is a inner loop that executes $O(E)$ times. In total we get $O(E \cdot V)$.