1.Definition and Examples

Contents/Index

@1. Definition and Examples

Definition

An adjunction consists of the following

• A pair of categories $\mathcal{C}$ and $\mathcal{D}$
• A pair of functors $F : \mathcal{C} \rightarrow \mathcal{D}$ and $G : \mathcal{D} \rightarrow \mathcal{C}$
• A natural transformation $\mu : I_C \rightarrow (G \circ F)$

Such that for each $\mathcal{C}$-object $X$ and $\mathcal{C}$-arrow $f : X \rightarrow G(Y)$ there is a unique $\mathcal{D}$-arrow $f^{\#} : F(X) \rightarrow Y$ such that the following triangle commutes:

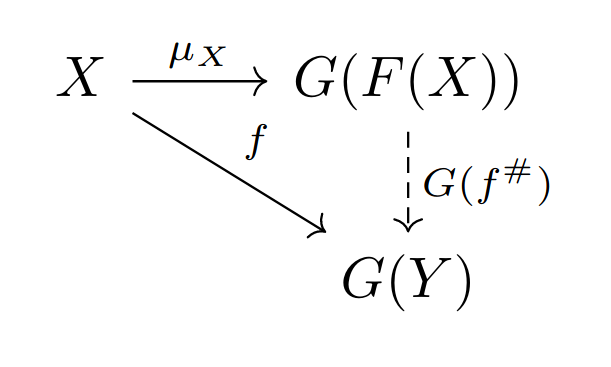
Note that $X,G(Y) \in \mathcal{C}$ and $F(X),Y \in \mathcal{D}$. $(F,G)$ is called an adjoint pair of functors, $F$ is the left adjoint of $G$, and $G$ is the right adjoint of $F$. The natural transformation $\mu$ is called the unit of the adjunction.

Example - Adjoints on lists

We can make a somewhat concrete example of adjoints. Consider the monoid $(List(S),*,[])$. That is the monoid of lists with elements of some set $S$. Let $f : S \rightarrow M$ be some function from the set $S$ to the monoid $(M,\cdot,e)$, where $M$ is the underlying set. Let $i$ be an injection function that takes $s \in S$ to the singleton list $[s]$. Then there is one, and only one, monoid homomorphism $$ f^{\#} : (List(S),*,[]) \rightarrow (M,\cdot,e) $$ for which the following diagram commutes

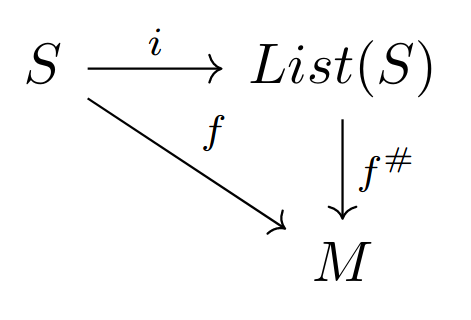
Proof. Let $f^{\#}$ be the function that takes a list $[s_1,s_2, ... , s_n]$ to the product $f(s_1) \cdot f(s_2) \cdots f(s_n)$ and the empty list $[]$ to $e$. This is clearly a homomorphism. Furthermore we have that the diagram of Figure2 commutes. We list these results

1. $f^{\#}([]) = e$
2. $f^{\#}([s_1,s_2, ... , s_n] * [t_1, t_2 , ... , t_n]) = f^{\#}([s_1, s_2 , ... , s_n]) \cdot f^{\#}([t_1, t_2 , ... , t_n])$
3. $f^{\#} \circ i = f$

Example - Adjoints on the length function on lists

The function $length : List(S) \rightarrow \mathbb{N}$ can be given by the following set of recursive functions

• $length([]]) = 0$
• $length(L * L') = length(L) + length(L')$
• $length(i(s)) = 1$

Where again $i$ is the injection that takes $s \in S$ to the singleton list $[s]$. The two first lines in the above recursive definition corresponds to a homomorphism from $(List(S),*,[])$ to $(\mathbb{N},+,0)$. The third line states that the diagram in Figure3 commutes. Here the $1$ function is a function that sends every element in the domain to $1 \in \mathbb{N}$.

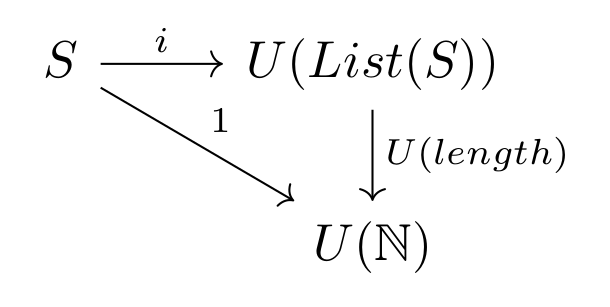
Figure3 has been extended with functors according to the definition of an adjoint. That is the functor $F$ is $List : \textbf{Set} \rightarrow \textbf{Mon}$. The functor $G$ is the forgetful functor $U : \textbf{Mon} \rightarrow \textbf{Set}$. The natural transformation $\eta$ is the family of functions $i_{S} : S \rightarrow List(S)$ - that is one function for each element in $s \in S$ that takes this element to the singleton list $[s]$.