Syntax

Contents/Index

Preface
@Syntax
Generating parser
The application

We need a parser. I have developed a liking for SLR parsers. So let's make one of those. We need a set of tokens

int = [0-9]+ float = [0-9]*,[0-9]+ id = [a-zA-Z]+ plus = + minus = - times = * divide = / power = ^ lpar = ( rpar = ) comma = ,

We need the id for built in functions such as sqrt.

Since I have already built a parser for propositional logic, Prop2Table, a parser that is very similar to this one, I will skip a lot of the details. Let us build the grammar

Exp \rightarrow Exp plus Exp Exp \rightarrow Exp minus Exp Exp \rightarrow Exp times Exp Exp \rightarrow Exp divide Exp Exp \rightarrow Exp power Exp Exp \rightarrow minus Exp Exp \rightarrow Call Exp \rightarrow Atom Call \rightarrow id lpar Args rpar Args \rightarrow Arg Args' | Args' \rightarrow comma Arg Args' | Arg \rightarrow Exp Atom \rightarrow lpar Exp rpar Atom \rightarrow float Atom \rightarrow int

With this grammar we can nest calls. That's pretty decent, I think. As we have done before: First we construct an NFA to use with the nfa2dfa converter. To do this we add a start productions and number all the productions (thus obtaining the expanded grammar).

#Transitions #[0] Exp' -> Exp start (A) -Exp>(B) ((B)) #[1] Exp -> Exp plus Exp (C) -Exp>(D) (D) -plus>(E) (E) -Exp>(F) ((F)) #[2] Exp -> Exp minus Exp (G) -Exp>(H) (H) -minus>(I) (I) -Exp>(J) ((J)) #[3] Exp -> Exp times Exp (K) -Exp>(L) (L) -times>(M) (M) -Exp>(N) ((N)) #[4] Exp -> Exp divide Exp (O) -Exp>(P) (P) -divide>(Q) (Q) -Exp>(R) ((R)) #[5] Exp -> Exp power Exp (S) -Exp>(T) (T) -power>(U) (U) -Exp>(V) ((V)) #[6] Exp -> Call (A1) -Call>(B1) ((B1)) #[7] Exp -> Atom (C1) -Atom>(D1) ((D1)) #[8] Exp -> minus Exp (F1) -minus>(G1) (G1) -Exp>(H1) ((H1)) #[9] Call -> id lpar Args rpar (I1) -id>(J1) (J1) -lpar>(K1) (K1) -Args>(L1) (L1) -rpar>(M1) ((M1)) #[10] Args -> Arg Args' (O1) -Arg>(P1) (P1) -Args'>(Q1) ((Q1)) #[11] Args -> ((R1)) #[12] Args' -> comma Arg Args' (S1) -comma>(T1) (T1) -Arg>(U1) (V1) -Args'>(W1) ((W1)) #[13] Args' -> ((A2)) #[14] Arg -> Exp (B2) -Exp>(C2) ((C2)) #[15] Atom -> lpar Exp rpar (D2) -lpar>(E2) (E2) -Exp>(F2) (F2) -rpar>(G2) ((G2)) #[16] Atom -> float (H2) -float>(I2) ((I2)) #[17] Atom -> int (J2) -int>(K2) ((K2))

We add epsilon transitions from every non-terminal transition to every production of that terminal

#added epsilon #[0] Exp' -> Exp start (A) -Exp>(B) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) ((B)) #[1] Exp -> Exp plus Exp (C) -Exp>(D) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) (D) -plus>(E) (E) -Exp>(F) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) ((F)) #[2] Exp -> Exp minus Exp (G) -Exp>(H) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) (H) -minus>(I) (I) -Exp>(J) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) ((J)) #[3] Exp -> Exp times Exp (K) -Exp>(L) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) (L) -times>(M) (M) -Exp>(N) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) ((N)) #[4] Exp -> Exp divide Exp (O) -Exp>(P) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) (P) -divide>(Q) (Q) -Exp>(R) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) ((R)) #[5] Exp -> Exp power Exp (S) -Exp>(T) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) (T) -power>(U) (U) -Exp>(V) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) ((V)) #[6] Exp -> Call (A1) -Call>(B1) -eps>(I1) ((B1)) #[7] Exp -> Atom (C1) -Atom>(D1) -eps>(A2) -eps>(E2) -eps>(G2) ((D1)) #[8] Exp -> minus Exp (F1) -minus>(G1) (G1) -Exp>(H1) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) ((H1)) #[9] Call -> id lpar Args rpar (I1) -id>(J1) (J1) -lpar>(K1) (K1) -Args>(L1) -eps>(O1) -eps>(R1) (L1) -rpar>(M1) ((M1)) #[10] Args -> Arg Args' (O1) -Arg>(P1) -eps>(B2) (P1) -Args'>(Q1) -eps>(S1) -eps>(A2) ((Q1)) #[11] Args -> ((R1)) #[12] Args' -> comma Arg Args' (S1) -comma>(T1) (T1) -Arg>(U1) -eps>(B2) (V1) -Args'>(W1) -eps>(S1) -eps>(A2) ((W1)) #[13] Args' -> ((A2)) #[14] Arg -> Exp (B2) -Exp>(C2) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) ((C2)) #[15] Atom -> lpar Exp rpar (D2) -lpar>(E2) (E2) -Exp>(F2) -eps>(C) -eps>(G) -eps>(K) -eps>(O) -eps>(S) -eps>(A1) -eps>(C1) -eps>(F1) (F2) -rpar>(G2) ((G2)) #[16] Atom -> float (H2) -float>(I2) ((F2)) #[17] Atom -> int (J2) -int>(K2) ((K2))

This we run through the converter to obtain shift actions. Now before we create the tables, let us decide on associativity and precedence. We get

precedence: plus:1 minus:1 times:2 divide:2 power:3 associativity: plus:left minus:left times:left divide:left power:right

From this we create the tables. First we calculating follow using the extended grammar and the Grammar2Set converter. With the follow sets we can obtain reduce actions as done in the prop2table project. With solved conflicts we get

Action Table

comma	divide	float	id	int	lpar	minus	plus	power	rpar	times	$
		s5	s6	s7	s8	s9
	r8					r8	r8	r8	r8	r8	r8
	r7					r7	r7	r7	r7	r7	r7
	s10					s11	s12	s13		s14	r1
											accept
r17	r17					r17	r17	r17	r17	r17	r17
					s15
r18	r18					r18	r18	r18	r18	r18	r18
		s5	s6	s7	s8	s9
		s5	s6	s7	s8	s9
		s5	s6	s7	s8	s9
		s5	s6	s7	s8	s9
		s5	s6	s7	s8	s9
		s5	s6	s7	s8	s9
		s5	s6	s7	s8	s9
r15	r15	s5	s6	s7	s8	r15	r15	r15	r15	r15	r15
	s10					s11	s12	s13	s27	s14
	s10					r9	r9	s13	r9	s14	r9
	r5					r5	r5	s13	r5	r5	r5
	s10					r2	r2	s13	r2	s14	r2
	s10					r3	r3	s13	r3	s14	r3
	r6					r6	r6	s13	r6	r6	r6
	r4					r4	r4	s13	r4	r4	r4
s28									r11
									s29
r13	r13					r13	r13	r13	r13	r13	r13
r14	r14					r14	r14	r14	r14	r14	r14
r16	r16					r16	r16	r16	r16	r16	r16
r15	r15	s5	s6	s7	s8	r15	r15	r15	r15	r15	r15
r10	r10					r10	r10	r10	r10	r10	r10
									r12

Goto Table

	Exp'	Exp	Call	Args	Arg	Atom
0	g4	g3	g2			g1
1
2
3
4
5
6
7
8		g16	g2			g1
9		g17	g2			g1
10		g18	g2			g1
11		g19	g2			g1
12		g20	g2			g1
13		g21	g2			g1
14		g22	g2			g1
15			g26	g24	g23	g25
16
17
18
19
20
21
22
23
24
25
26
27
28			g26	g30	g23	g25
29
30

And this is actually it. When the parser parses a string, it does so the same way as one would traverse the resulting syntax tree. That is: we just evaluate with the parser. So in order to get a deeper understanding let us draw a tree. Say we have

1 + 2 + 3 * 4 * 5

For this expression we get the tree

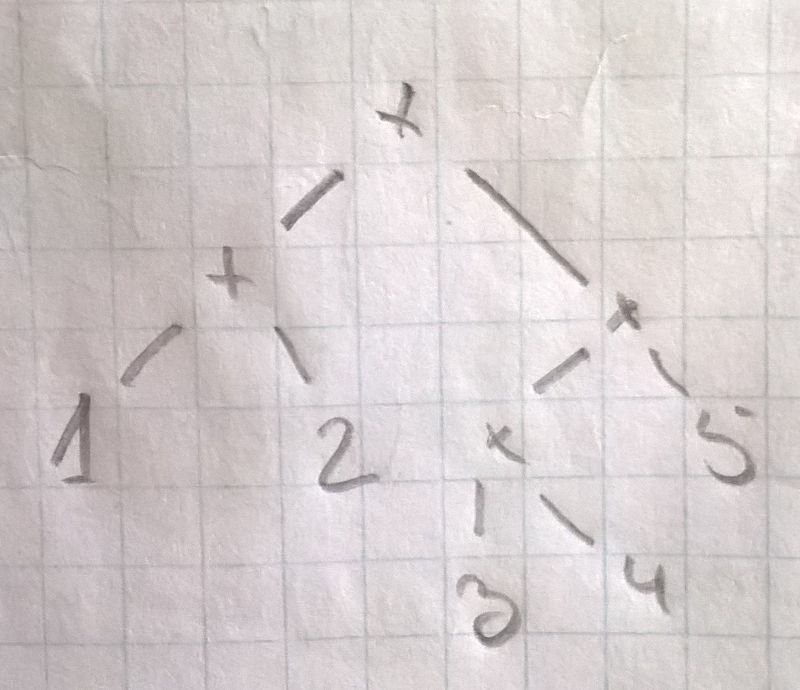
Which we traverses buttom up, or depth first, and we have a valuated expression that respects the precedence and associativity rules. This is excatly the way the SLR parser traverses the expression.