MergeSort

Paradigm: divide, conquer, combine.

Mergesort merges lists into atomic parts and then combines them back into a sorted list. Ex [5,3,10,2] → [5,3],[10,2] → [5],[3],[10],[2] → [3,5],[2,10] → [2,3,5,10]

The code for merge is

Merge(A,p,q,r) n_{1} = q - p + 1 n_{2} = r - q let L[1 ... n_{1} + 1] let R[1 ... n_{2} + 1] for i = 1 to n_{2} L[i] = A[p + i - 1] for j = 1 to n_{2} R[j] = A[q + j] L[n_{1} + 1] = ∞ R[n_{2} + 1] = ∞ i = 1 j = 1 for k = p to r if L[i] \leq R[j] A[k] = L[i] i = i + 1 else A[k] = R[j] j = j + 1

That is it merges two lists into one sorted:

{1,4},{2,5} {4},{2,5} \rightarrow {1} {4},{5} \rightarrow {1,2} {5} \rightarrow {1,2,4} {} \rightarrow {1,2,4,5}

And the code for merge-sort is

Merge-Sort(A,p,r) if q < r q = ceil((p + r) / 2) Merge-Sort(A,p,q) Merge-Sort(A,q + 1,r) Merge(A,p,q,r)

Ways to calculate time complexity on recursive methods

• Recursion trees (used to guess)
• Master method (used as a shortcut)
• Substitution (Universal)

Mergesort equation $$ T(n) = \begin{cases} T(1) & n = 1 \\ 2 T(n/2) + n & n > 1 \end{cases} $$

The recursion tree can be drawn for 3 levels as follows

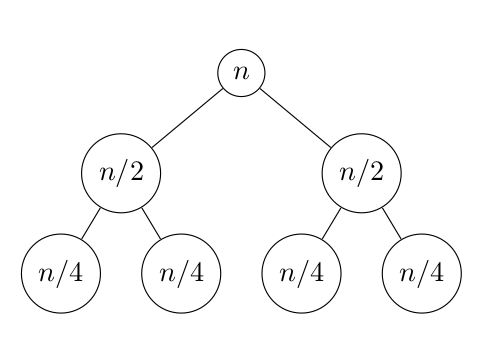
Which seems like $O(n lg(n))$. Let's proof that by using the substitution method. So guess $c \cdot n \cdot lg(n)$. Base cases are $n = 2$ and $n = 3$ - we need to chose two to avoid relying on $n = 1$. $$ T(2) = 2 \cdot 1 + 2 \leq c \cdot 2 $$ and $$ T(3) = 2 \cdot 3/2 + 3 \leq c \cdot 3 $$ And for the induction step. Assume strongly that $T(n - 1) \leq c(n - 1)lg(n -1)$, that is for all $n_0 \leq n - 1$ and especially $n/2$. Now we get $$ T(n/2) \leq (n/2) \cdot c \cdot lg(n/2) \Rightarrow \\ 2T(n/2) \leq n \cdot c \cdot lg(n/2) \Rightarrow \\ 2T(n/2) + n \leq n \cdot c \cdot lg(n / 2) + n \Rightarrow \\ T(n) \leq n \cdot c(lg(n) - lg(2)) + n \Rightarrow \\ T(n) \leq c \cdot n \cdot lg - c \cdot n + n \leq c \cdot n \cdot lg(n) $$ for $c \geq 1$, and we are done.