Sektion 2.1

Opgave 1

Giv en kortere beskrivelse af mængderne.

a) $[2,4] \cup [3,6] = \lbrace x \in \mathbb{R} | 2 \le x \le 6\rbrace = [2,6]$

b) $[2,4] \cap [3,6] = \lbrace x \in \mathbb{R} | 3 \le x \le 4\rbrace = [3,4]$

c) $(-3,4) \cup [-2,1) = [-2,4)$

d) $[4,7] \cap \mathbb{N} = \lbrace 4,5,6,7\rbrace$

e) $(-\infty,1) \cup (-1,\infty) = \mathbb{R}$

f) $(2,4) \setminus (1,3) = [3,4)$

Opgave 2

Giv en kortere beskrivelse af mængderne.

a) $\emptyset \cup (1,5) = (1,5)$

b) $\emptyset \cap (1,5) = \emptyset$

c) $\emptyset \cup (1,5) = (1,5)$ - umiddelbart magen til a)

d) $\mathbb{N} \setminus \mathbb{R} = \emptyset$

Opgave 4

Tegn graferne til funktionerne (Maple to the recue).

a) $f(x) = |x - 2|$$ : plot(|x - 2|)

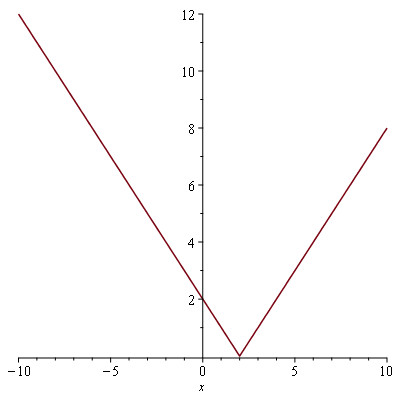
Analyse: grafen giver 0 når x = 2. Derudover er den magen til grafen for $f(x) = |x|$.

b) $f(x) = \sqrt |x|$ : plot(sqrt(|x|))

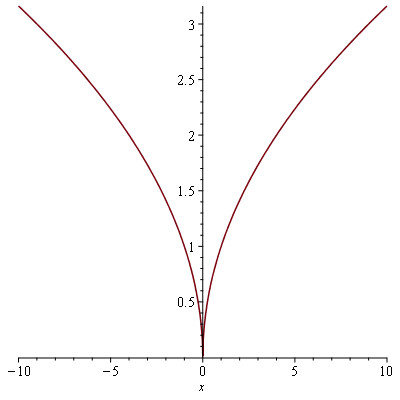
Analyse: en spejlvendt klon af √x. Dette giver fint mening da for $x \lt 0$ gælder: $|x| = -x$.

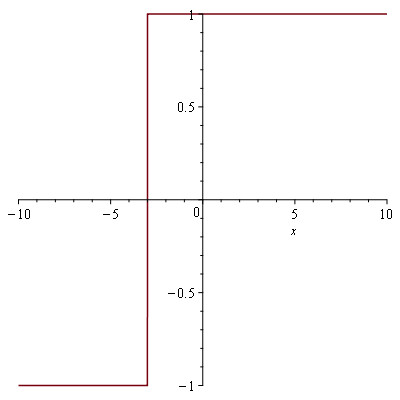
c) $f(x) = \frac{|x + 3|}{x + 3}$ : plot((|x + 3|)/(x + 3)

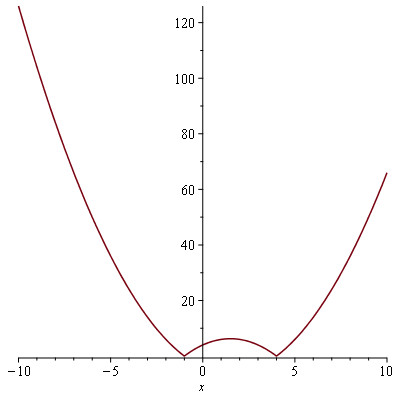
d) $f(x) = |x + 1||x - 4|$ : plot(|x+1|*|x-4|)

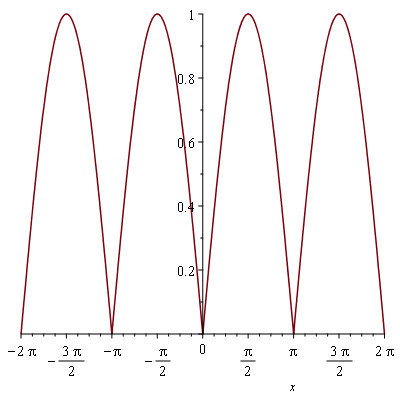
e) $f(x) = |sin x|$ : plot(|sin(x)|)

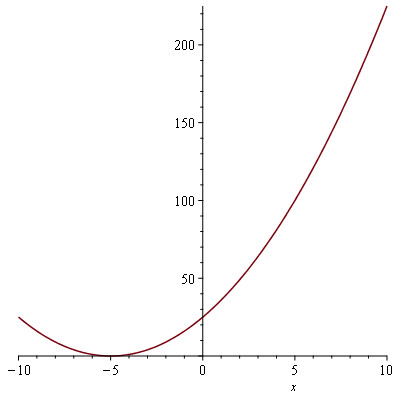
d) $f(x) = |x + 5|^2$ : plot(|x + 5|^2)

Opgave 5

Løs ulighederne.

a) $|x - 2| \lt |x + 3|$ - følg hint. $$ |x - 2| \lt |x + 3| \Rightarrow \\ |x - 2|^2 \lt |x + 3|^2 \Rightarrow \\ x^2 + 4 - 4x \lt x^2 + 9 + 6x \Rightarrow \\ -5 \lt 10x \Rightarrow \\ -1/2 \lt x $$

b) $|x^2 -2x -8| \gt 8$ - følg hint. $$x^2 - 2x - 8 \gt 8$$ løs: $x^2 - 2x - 16 = 0$ $$ d = 2^2 - 4\cdot1\cdot(-16) = 4 + 64 = 68 \\ x_1 = 1 + \sqrt 17, x_2 = 1 - \sqrt 17 $$ løs: $x^2 - 2x - 8 = -8$ $$ x^2 - 2x - 8 = -8 \Rightarrow \\ x^2 -2x = 0 \Rightarrow \\ x_1 = 0, x_2 = 2 $$ løsning: for $(x \gt 0 \land x \lt 2) \lor (x \lt 1 - \sqrt 17) \lor (x \gt 1 + \sqrt 17)$ gælder b)

Opgave 9

Vis at for alle tal $x, y, z$ gælder $|x - y| \le |x - z| + |z - y|$
Bevis: $$|x - y| = |x - z + z - y| \le |x - z| + |z - y|$$

Opgave 10

Vis ved induktion over $n$ at $$ |a_1 + ... + a_n| \le |a_1| + ... + |a_n| $$ Induktionsstart: $$ |a_1| \le |a_1| \\ |a_1 + a_2| \le |a_1| + |a_2| $$ Induktionsskridt:
Lad $|a_1 + ... + a_n| \le |a_1| + ... + |a_n|$: $$ |a_1 + ... + a_n + a_{n + 1}| \le \\ |a_1 + ... + a_n| + |a_{n + 1}| \le \\ |a_1| + ... + |a_n| + |a_{n + 1}| $$

Opgave 12

Vis uligheden $\sqrt av \le \frac{a + b}{2}$ gælder for alle a,b ≥ 0.
Lemma 2.1.1: $$ (a - b)^2 \ge 0 \Rightarrow a^2 + b^2 - 2ab \ge 0 \Rightarrow a^2 + b^2 \ge 2ab $$ Løsning:
$$ a^2 + b^2 \ge 2ab \Rightarrow \\ \frac{a^2 + b^2}{4} \ge \frac{ab}{2} \Rightarrow \\ \frac{a^2 + b^2 + 2ab}{4} \ge ab \\ \frac{a + b}{2} \ge \sqrt ab $$