Sektion 3.2

Opgave 1

Lav en figur der viser hvor tallene ligger i det komplekse plan.

a) $1 + i$

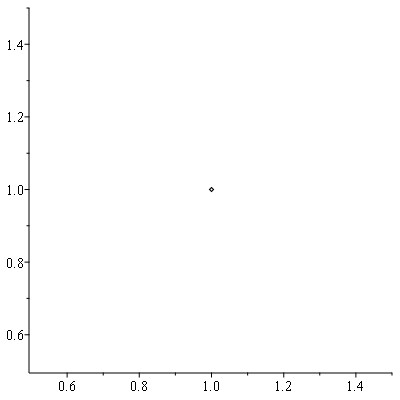
b) $1 - i$

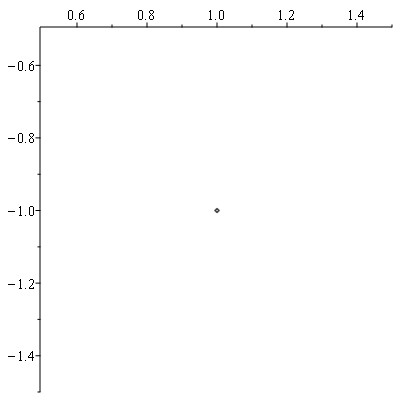
c) $-1 + i$

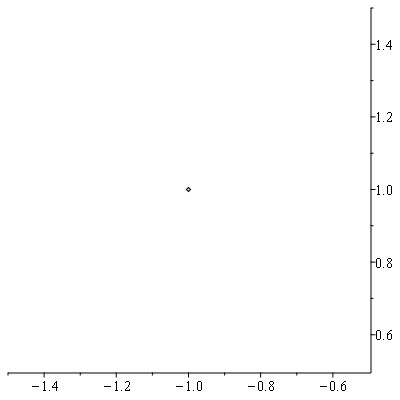
d) $-1 - i$

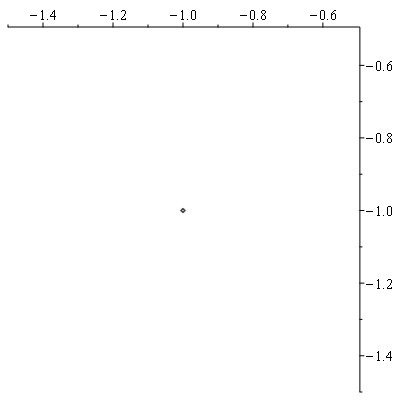
Opgave 3

Find modulus og argument til følgende.

a) $i : r = \sqrt(0^2 + 1^2) = 1, cos \theta = 1 \Rightarrow \theta = 0$

b) $-i : r = \sqrt(0^2 + (-1)^2) = 1, cos \theta = 1 \Rightarrow \theta = 0$

c) $1 + i : r = \sqrt(1^2 + 1^2) = \sqrt 2, cos \theta = 1/\sqrt 2 \Rightarrow \theta = \pi/4$

d) $-3 : r = \sqrt((-3)^2 + 0^2) = 3, cos \theta = -3/3 = -1 \Rightarrow \theta = \pi$

e) $1 + i\sqrt 3 : r = \sqrt(1^2 + \sqrt 3^2) = 2, cos \theta = 1/2 \Rightarrow \theta = \pi/3$

Opgave 5

Skriv følgende komplekse tal på formen a + ib.

a) $r = 4, \theta = \pi/2 : (cos \pi/2)4 + i(sin \pi/2)4 = 4i$

b) $r = 1, \theta = \pi/4 : (cos \pi/4) + i(sin \pi/4) = i(\sqrt 2/2)$

c) $r = 2, \theta = \pi/6 : 2(cos \pi/6) + i2(sin \pi/6) = \sqrt 3 - i$

d) $r = 1/2, \theta = 3\pi/2 : 1/2(cos 3\pi/2) + i(1/2)(sin 3\pi/2) = - 1/2i$

Opgave 12

Vis at de to komplekse tal, $z$ og $w$, er normale på hinanden hvis og kun hvis $z/w$ er et rent imaginært tal. Hvornår er $z$ og $w$ paralelle?
Mod højre:
Lad $x \in \mathbb{R}, x \ne 0$ $$ \frac{a + ib}{x(b - ai)} = \\ \frac{ab + ia^2 + ib^2 + abi^2}{x(b^2 + a^2)} = \\ \frac{ia^2 + ib^2}{x(a^2 + b^2)} = \\ i(1/x) $$ Mod venstre:
Lad $x \in \mathbb{R}, x \ne 0, Lad z = a + ib, w = c + id$ $$ \frac{z}{w} = \\ ix \Rightarrow \frac{a + ib}{c + id} = \\ ix \Rightarrow \frac{b - ai}{c + id} = \\ x \Rightarrow b - ai = \\ x(c + id) \Rightarrow \frac{b}{x} - i\frac{a}{x} = \\ c + id = w $$ Og vi er altså kommet frem til det ønskede.

To vektorer er paralelle hvis deres determinant er lig 0. Hvis $z = a + ib$ og $w = c + id$, skal der altså gælde at $aid - cib = 0$