Lav noget der regner del 1 - MBOL #1
23.05.2017
Solen skinner, ja, så lad os lave noget der regner. For godt to år siden lavede jeg en beretning om en lommeregner jeg havde lavet. Den gang kunne jeg kikke tilbage på min første lommeregner og grine uhæmmet, den kan ses her. Nu kan jeg tilgengæld kikke tilbage på min sidste lommeregner og grine måske ikke nær så uhæmmet, men alligevel. Den kan ses her:
I mellemtiden er det gået op for mig at det at lave en regnemaskine i et programmeringssprog faktisk har en del at gøre med det at lave et programmeringssprog. Og det har jeg besluttet mig for at lave nu, så hermed præsenteres MBOL . MrBirkmandsOperatorLanguage. Jaja, lad ikke titlen snyde.
For to år siden lavede jeg min regnemaskine på følgende måde i JS. Observer følgende stykke; $$1 + 2 + 3 + 4 \cdot 5 _{1}$$
Hvad giver det? Det giver: 1 + 2 = 3 + 3 = 6 + 4*5 = 6 + 20 = 26. Vi introducerer regnehierarki eller præcedens, man ganger før man plusser. En anden måde at udtrykke stykket på kan være: $$(((1 + 2) + 3) + (4 * 5))$$ eller $$(+ (+ (+ 1 2) 3) (* 4 5))$$ Hvor operatorerne i sidste står som præfiks. Lad os lige huske på disse notationer og vende tilbage til min to år gamle løsning. Tag ovenstående stykke, for to år siden løste jeg det ved dele det op i to lister:
var tal = [1,2,3,4,5]; var op = [+,+,+,*];Herefter pløjede jeg dem igennem, tog ét element ud af op og to ud af tal, regnede de to tal sammen, erstattede det sidste tal med resultatet og fortsatte. ComCalc, min 2 år gamle regner, lavede selvfølgelig et gennemløb først og kikkede efter * eller /, derefter et gennemløb hvor den kikkede efter + eller -. På den måde blev præcedenses bevaret.
Jeg synes ikke det er nogen dårlig løsning, den fungerer da der altid er én mindre operator end antal tal eller operander i et korrekt angivet regnestykke. Problemet kommer når parenteser introduceres. Så vidt jeg lige kan se, løste jeg parenteser ved at lave en separat liste med dem og funktioner som regnes først. Og herefter bliver det noget indviklet.
Den overordnede ide var og er nu i hvert fald den samme:
- Tag et stykke, angiv operatorer og tal, disse kaldes leksemer eller tokens.
- Lav en eller anden struktur ud af dem, for to år siden to lister.
- Saml strukturen til et resultat.
Det første og sidste punkt er faktisk de nemmeste, det i mellem er til gengæld det vigtigste for at bevare en overskuelighed. Så, without further ado, her et syntakstræ:
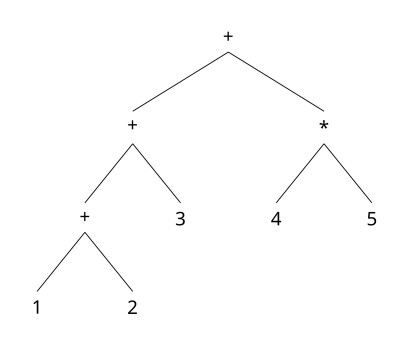
Træet kommer af noget der hedder produktionsregler, for plus og gange kan de se således ud: $$ add \rightarrow add + multi | multi \\ multi \rightarrow multi \cdot tal | tal \\ tal \rightarrow {0,1,2,3,4,5,6,7,8,9} | tal \& tal $$ Hvor & betyder konkatenering. Ideen er faktisk hentet fra lingvistikken, det hedder en kontekstfri grammatik, og den fungerer som følgende: tag 1 + 2 + 3 + 4 ⋅ 5. Bagfra fås: 4 ⋅ 5 er multi ⋅ tal, 5, og multi herunder er tallet 4. Disse to samles til multi. Vi kikker på næste tegn som er +, dette har multi på højre og en add på venstre som har 3 på højre og en ny add på venstre. Osv.
De tre produktionsregler er rekursive, de kan returnere sig selv. Reglen er den der står på venstre side af pilene, disse kaldes ikke-terminaler. På højre side står resultaterne. De resultater der ikke fører videre, i dette tilfælde mængden af tal, kaldes terminaler. Det hele ender jo med dem. | angiver eller, add kan altså have formen add + multi eller multi.
Reglerne medfører træet på tegningen. De kan udvides til de fundamentale regneoperationer: $$ add \rightarrow add + multi | add - multi | multi \\ multi \rightarrow multi \cdot tal | multi / tal | tal \\ tal \rightarrow (add) | {0,1,2,3,4,5,6,7,8,9} | tal \& tal \\ $$ Hvor (add) er parenteser. Hvis vi kan lave en maskine der bygger et træ ud fra de tre produktionsregler, kan vi let regne det ved feks. at benytte en form for indorder-tree-walk algoritme:
var inorderTreeWalk = function(node){ if(node === null){ return; } inorderTreeWalk(node.left); document.write(node.value); inorderTreeWalk(node.right); }Parseren er nøglepunktet, men vi må nok hellere starte med at bygge en leksikal anlyseting. Så følg med.